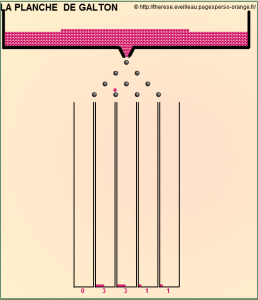
This week we looked at an online simulation of the Galton board (or Bean Machine), which is a device where beads are dropped from a funnel at the top through ranks of nails.
Each time a bead strikes a nail it has a 50% chance to veer left and a 50% chance to veer right.
Each bead eventually drops in one of the column A, B, C, D or E.
1. Do you think the probabilities for a bead to land in A,B,C,D or E are equal ?
2. If not which column has the highest probability ?
3. Can you do a computer simulation of 10,000 beads dropping in a Galton
board using scratch or Python ?