Month: March 2017

A cryptarithm is a type of mathematical puzzle in which the digits in numerical calculations are replaced by letters of the alphabet.

Alphametics are cryptarithms in which letters form meaningful words, often in meaningful phrases. There are only a few simple rules for these puzzles:

1. The same letter always stands for the same digit, and the same digit is always represented by the same letter. So if a P stands for a 2, every P in the puzzle is a 2. If a 3 is represented by a K, every 3 in the puzzle will be a K.

2.The digit zero is not allowed to appear as the left-most digit in any of the numbers in the puzzle. For example, if the word FOOD represents an addend in a puzzle, the F may not be a zero.

3.Most alphametics have unique solutions (there is only one possible answer).

One of our favourite websites is brilliant.org, so today we spent time on it solving different puzzles. You have to register an account, but then you have access to great mathematics and other science questions.

Here is one of the puzzles we worked on:

As it was Pi Day on Tuesday (14th of March is 3.14 in American style date!) we thought we would try and estimate the value of Pi by simulating throwing darts randomly at a square dartboard like below and seeing how many land inside the circle.

One way to do this is to generate a random point by typing the following in the input bar.

(RandomUniform[-1, 1], RandomUniform[-1, 1])

This will generate a point with x coordinate inbetween -1 and 1 and y coordinate inbetween -1 and 1.

Then right click on the point and select “Trace On”.

In the View menu there is a command called “Recompute All Objects”. The shortcut for this is to hold down Ctrl and press R.

You should see your random point going to different places in the screen. You can do this say 80 times.

Alternatively, you can create 80 points on a spreadsheet with the Random Uniform command and then “Create List of Points”. See here for a working applet with this method.

Either way you can now estimate the value of Pi!!!

Count the number of points inside the circle
Divide this by 80 to get the proportion of points that are inside the circle.
Area of the circle is π * 1² = π
Area of square is 2*2=4
So this proportion should be π/4.
So if we multiply our proportion by 4 we get an estimate for π.

The more points you use the better the estimate will be.

Good luck, and happy Pi Day!

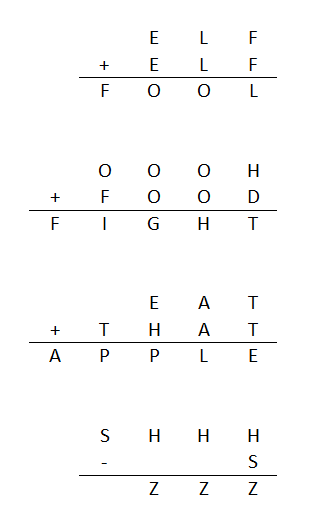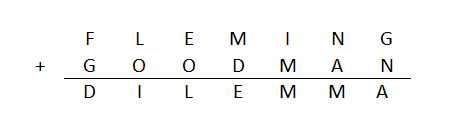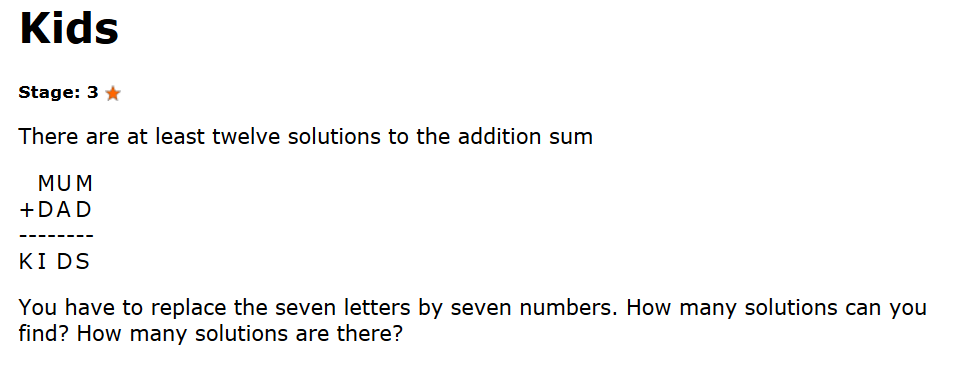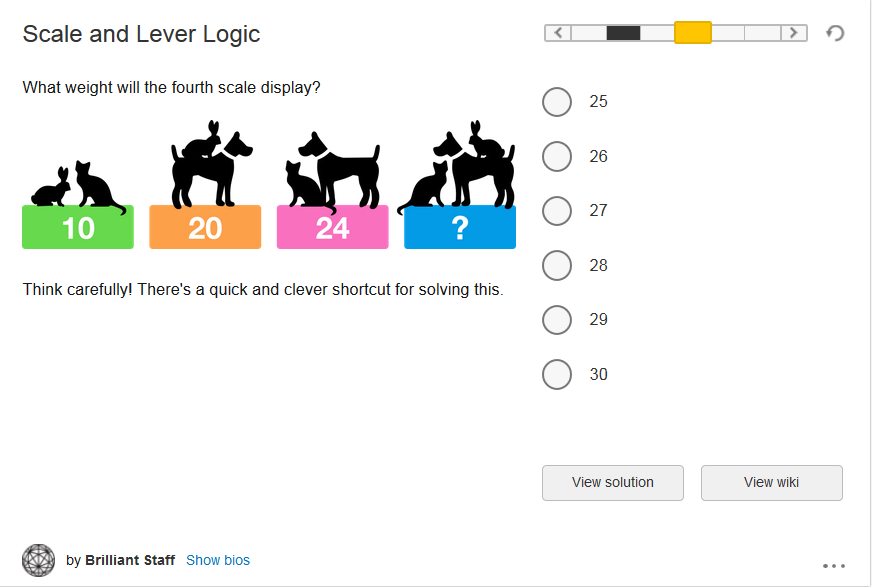
Think of an positive integer.

If it is equal to 1, stop.

If it is even, divide it by 2.

If it is odd, multiply it by 3 and add 1.

With the new number you get, repeat the instructions above.

If you picked the number 6, your sequence would look like this:

3, 10, 5, 16, 8, 4, 2, 1

Did your sequence end up at 1? Mathematicians have guessed (hypothesised) that all starting choices will eventually end up at 1, but no one has been able to prove this. If you can find just one example that disproves this theory then you could claim a prize of 120 million Japenese Yen!  Here is a fun example of a counterexample that took a long time to find.

Try a few starting numbers by hand. Then you could try and use the power of a spreadsheet such as Geogebra, or by writing some code on Python and let the computer do the hard work for you!

Open up Geogebra.

You will need to use the Mod  command:

Mod[ <Dividend Number>, <Divisor Number> ]

to check if the number is even.

and the If command:

If[ <Condition>, <Then>, <Else> ]

to choose what to do if it is even and what to do if it is odd.

Put together, here is the formula you should put into cell A2, once you have put a starting number in A1.

=If[Mod[A1, 2] == 0, A1 / 2, A1*3 + 1]

Then just hover your mouse pointer in the bottom right corner and click the left button and hold down and drag down lots of cells. You should see the sequence appear.

If you want to be super clever you could try and combine two If statements so that if the cell was equal to 1 it would stop calculating and just say “STOP”.

You could also try this activity on Python, click on the menu bar on the top left to make it full screen.

Good luck!