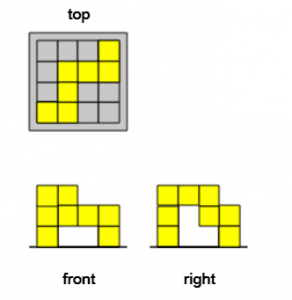
We used this website to solve a series of challenges where you start with front, side and top elevations to build the full picture of 3D shape – building up to using only two views and silhouettes.

We used this website to solve a series of challenges where you start with front, side and top elevations to build the full picture of 3D shape – building up to using only two views and silhouettes.
In pairs we played the following game a couple of times.
One person is heads (player 1), the other person is tails (player 2). Toss the coin a maximum of 10 times, player 1 gets a point if the coin lands on heads, and player 2 gets a point if the coin lands on tails. If one person becomes three points ahead of the other the game stops and they win. If no one is 3 points ahead after ten tosses the game is a tie.
Which of the following scores are impossible in this game and why? 5-2, 7-4, 6-2
Think of ways the game could end in a tie.
What is the chance of winning this game?
This following table will help.
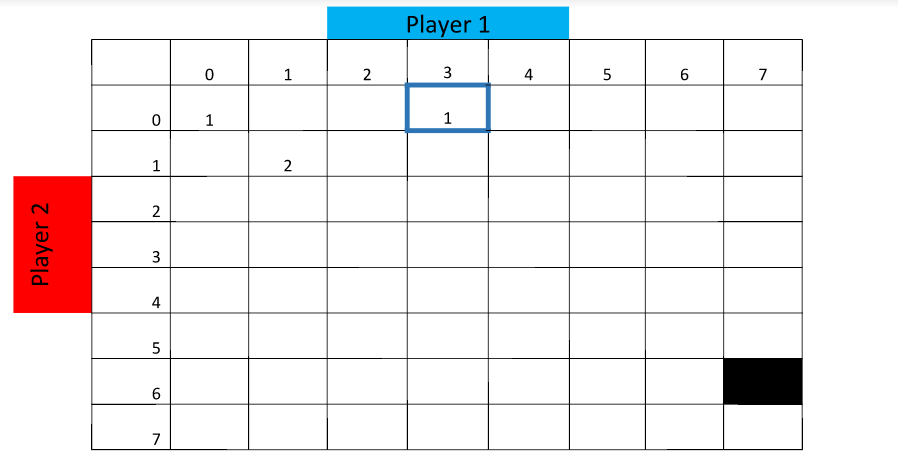
Fill in the table shading out impossible final scores, highlighting winning final scores for Player 1 and Player 2, and highlighting final scores which indicate a draw.
Then write in each box how many ways there are to end up at each score.
A few boxes have been filled in – for example 3-0 is a winning score for player 1, and there is only 1 way to get to that score (1-0 then 2-0 then 3-0). There are two ways to get to a score of 1-1 (0-1 then 1-1 or 1-0 then 1-1). There is a 1 in the 0-0 box as there is just one way to start the game.
See here for the solution, contained in an excellent presentation by Alex in the Further Maths class in PAL. This puzzle is the starting point for analysing how likely you are to win a tennis match if you only have a one third chance of winning each point. The idea and diagrams in the presentation were taken from the book Game, Set and Math by Ian Stewart.
Unit fractions are fractions that are written in the form 1⁄n.
Today’s challenge is to find sums of different unit fractions that are equal to another unit fraction.
For example: 1⁄2 = 1⁄3 + 1⁄6
Let’s see if there is a rule: which of the following are right and which are wrong?
1⁄2 = 1⁄10 + 1⁄20
1⁄3 = 1⁄4 + 1⁄12
1⁄3 = 1⁄7 + 1⁄21
1⁄4 = 1⁄5 + 1⁄20
The next challenge is to spot the pattern in these sums of unit fractions:
1⁄6 = 1⁄7 + 1⁄42
1⁄6 = 1⁄8 + 1⁄24
1⁄6 = 1⁄9 + 1⁄18
1⁄6 = 1⁄10 + 1⁄15
Bear in mind that 1⁄6 = 1⁄12 + 1⁄12 is wrong because both unit fractions are the same.
Try and use this to example to find all the unit fraction sums that add up to 1⁄18.
What if original fraction is not a unit fraction?
Egyptians had a tendency to write fractions as sums of unit fractions.
Of course, there is an infinite number of ways to do this. Let’s take for example.
2⁄3 = 1⁄3 + 1⁄4 + 1⁄12
2⁄3 = 1⁄3 + 1⁄5 + 1⁄20 + 1⁄12
2⁄3 = 1⁄4 + 1⁄12 + 1⁄7 + 1⁄42 + 1⁄31 + 1⁄930 + 1⁄21 + 1⁄420 + 1⁄13 + 1⁄156
Etc.
But how about expressing non unit fractions as sums of two unit fractions? Here is one example:
2⁄3 = 1⁄2 + 1⁄6
But can all fractions with numerator 2 be written as the sum of just 2 unit fractions? Can you prove it?
Let’s finish off with the greedy algorithm. This algorithm, which was developed by Fibonacci, allows you to quickly find a non-unit fraction as the sum of several unit fractions.
For example, let’s take 11⁄12. The first step is to find the largest unit fraction below the other fraction. In this case, that fraction is 1⁄2. Then, you should subtract 1⁄2from 11⁄12, which gives 5⁄12. This means that 11⁄12 = 1⁄2 + 5⁄12 . Repeat this with 5⁄12 and you should get:
11⁄12 = 1⁄2 + 1⁄3 + 1⁄12
If you would like to learn more, you can to the NRICH website with these links:
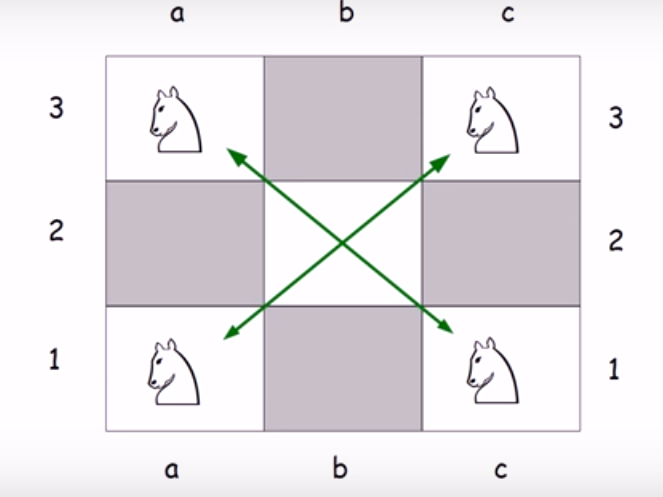
The challenge this week is to switch round the four knights as shown above, using only regular knights chess move (L shape – one along two up/down, or two along one up/down). Two knights can’t occupy the same space so you will need to be careful!
For an interesting discussion of the solution see this video .

Here is probably the hardest puzzle we’ve looked at so far in maths club …
Two perfect logicians, Sam and Polly, are told that integers x and y have been chosen such that 1 < x < y and x+y < 100. Sam is given the value x+y and Polly is given the value xy.
They then have the following conversation.
Polly: I cannot determine the two numbers.
Sam: I knew that.
Polly: Now I can determine them.
Sam: So can I.
Given that the above statements are true, what are the two numbers?
Starting points:
Before Polly and Sam say anything:
What is the range of numbers Sam could be given?
What is the range of numbers Polly could be given?
What special type of number can the product of x and y never be?
What about the square of these numbers?
After Polly’s first statement:
Give two examples of products that Polly can not be given.
After Sam’s first statement:
Give two examples of sum’s that Sam can not be given.
Next steps …
At this point you probably want to start using a computer to generate a list of numbers that they could be given.

This puzzle comes from Alex Bellos’ column in the Guardian. It has been adapted from one by Prem Prakash, an electrical engineer from Bangalore, India, who has taken early retirement to develop puzzle-based teaching workshops.
You and your two friends Pip and Blossom are captured by an evil gang of logicians. In order to gain your freedom, the gang’s chief, Kurt, sets you this fearsome challenge.
The three of you are put in adjacent cells. In each cell is a quantity of apples. Each of you can count the number of apples in your own cell, but not in anyone else’s. You are told that each cell has at least one apple, and at most nine apples, and no two cells have the same number of apples.
The rules of the challenge are as follows: The three of you will ask Kurt a single question each, which he will answer truthfully ‘Yes’ or ‘No’. Every one hears the questions and the answers. He will free you only if one of you tells him the total number of apples in all the cells.
Pip: Is the total an even number?
Kurt: No.
Blossom: Is the total a prime number?
Kurt: No
You have five apples in your cell. What question will you ask?
See here for the solution.
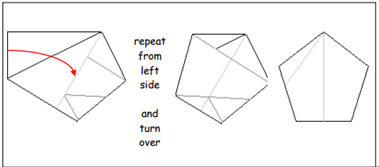
Today we looked at how we can transform a blank sheet of A4 paper into many different shapes such as an equilateral triangle and a kite. To do so you can either try to figure it out yourself or you can follow the Origami instructions for each different shapes.
If you have anymore interesting ideas please share them in the comment section below and if you want an extra challenge try proving that all of these folds actually give regular shapes bearing in mind the fact that the ratio of the sides in an A4 paper is 1:root 2
This week, we looked at three seemingly unrelated problems which all ended up being related to binary numbers.
The first is about Russian multiplication. Take, for instance 22 x 19. Multiply the left side by 2 every time and divide the right side by 2, and do this until the right side is equal to 1. If, while you do this, you ever get a decimal number on the right side, round down to the next integer.
e.g.
| 22 | 19 |
| 44 | 9 |
| 88 | 4 |
| 176 | 2 |
| 352 | 1 |
The next step is to get rid of all the lines with an even number on the right side, which leaves us with 22, 44 and 352 on the left side. Now we know that 22 x 19 = 418. What do you notice when you add 22, 44 and 352? Now try this with other multiplications. Does it still work? If it does, can you explain why it works?
Here is a website that explain this more fully:
https://www.basic-mathematics.com/russian-peasant-multiplication.html
The second problem we looked at today was all about magic cards or maths busking. Have a look at the following cards:
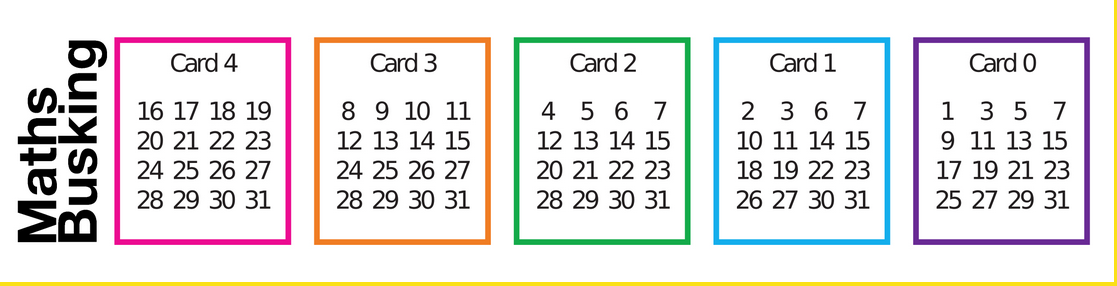
You can do the following trick with them. You ask someone to tell you which colour cards their birthdate appears on. You can straightaway say what their birthdate is. Can you guess how? It is not by learning all the numbers on the cards. One clue is to look at the first number in each card. Can you spot a pattern? Again, here is a website to help you:
http://www.mathmaniacs.org/lessons/01-binary/Magic_Trick/
Extension: If you add one more card, with how many more numbers can you do the trick with?
The final puzzle of today is about poisoned wine bottles. This is the story:
The King of a small country invites 1000 guests to his annual party.
Each guest brings the King a bottle of wine. Soon after, the Queen discovers that one of the guests is trying to assassinate the King by giving him a bottle of poisoned wine. Unfortunately, they do not know which guest, nor which bottle of wine is poisoned.
Just a single drop of the poisoned wine would kill the King.
The King has 10 prisoners in his dungeon. He decides to use them as taste testers to determine which bottle of wine contains the poison.
The poison when taken has no effect on the prisoner until exactly 24 hours later when the infected prisoner suddenly dies. The King needs to determine which bottle of wine is poisoned by tomorrow so that the festivities can continue as planned. Hence he only has time for one round of testing. How can the King administer the wine to the prisoners to ensure that 24 hours from now he is guaranteed to have found the poisoned wine bottle?
As we have seen with a lot of Maths Club problems, sometimes the first step is try with smaller numbers. For instance, instead of using 10 prisoners, we could say that there are 500 prisoners. So how could we test this now? Once you have figured this out, you could try with less and less prisoners. Now, we can solve the puzzle:
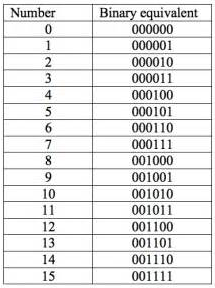
First, let’s line up our 10 prisoners and label them. Also label the wine bottles 0–999 so we can tell them apart.

Label each bottle with both its decimal number and binary equivalent.
decimal=binary
0=0000000000
1=0000000001
2=0000000010
3=0000000011
4=0000000100
5=0000000101
6=0000000110
7=0000000111
8=0000001000
9=0000001001
10=0000001010
etc
Now each bottle serves as a code describing which prisoners are to drink from it. In this system, a one means the prisoner drinks from it, a zero means the prisoner doesn’t.
For example, only Prisoner J should drink from bottle one since its binary is 0000000001. Whereas, Prisoners I and G should drink from bottle ten whose binary is 0000001010 because it has 1’s in the columns that match up with prisoners I and G.
Continue this process until you have given out sips of wine from every bottle. After 24 hours, line up the prisoners in order and note which ones have been poisoned with ones and mark the rest with zeros. Convert this number back into decimal to reveal which bottle was poisoned.
Extension: If there were 2000 bottles, how many prisoners would you need?
If you would like to learn to learn more about binary, check out this website:
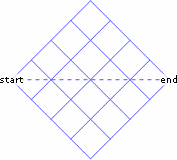
This week’s problem is all about counting the number of paths from one point to another on a 4 by 4 grid.
You can only travel in these directions

Here is one acceptable path:
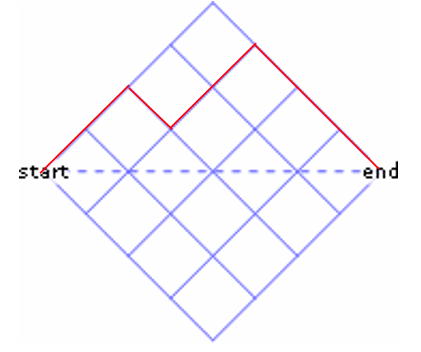
So how many such paths are there? First off, in which of these ranges do you think the answer lies:
< 20
20 – 40
40 – 60
60 – 80
80 – 100
>100
A first tip on how to solve this is to look at what is going on with smaller grids. Why don’t we start with a 1 by 1 grid? How many different paths are there between the starting point and the end point? Once we have done that, we can place the data on our larger grid.
After doing this a few times, does a pattern start to emerge?
Here is a website that shows all the solutions and an explanation of how the problem works, if you would like to learn more.