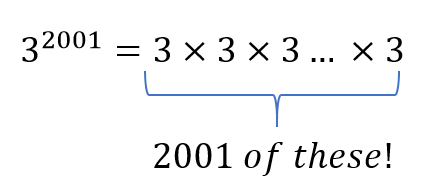
3 to the power of 2001 is a very big number (954 digits long!!). A regular calculator will not be able to calculate it.
Without calculating the value of this number, can you find the remainder when it is divided by 7?
For more explanation see the English and French versions of the puzzle.
And here are the solutions in English and French.
This problem was posted originally on the Nrich website .