Inspired by this fantastic numberphile video with Ben Sparks we are exploring the sequence of proper factors of numbers.
Aliquot 1
Aliquot 2
Inspired by this fantastic numberphile video with Ben Sparks we are exploring the sequence of proper factors of numbers.
Aliquot 1
Aliquot 2
Today we worked on challenging fraction questions sticking to ancient Egyptian methods – only unit fractions and you can’t repeat a fraction.
For example, can the following be expressed as a sum of distinct unit fractions?

This led to the greedy algorithm and some programming on excel:
See here for all the details and solutions.

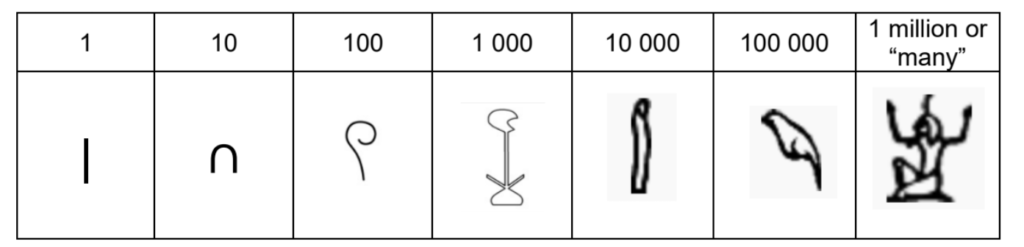
We are counting in whole numbers always starting at the number 1.
1,2,3,4, …
Schur numbers tell you the highest number that you can count to using k different colours before you’re forced to have an all same-coloured solution to a + b = c.
Example
Is this a valid colouring for k = 3 (3 colours)?

No, because 2 + 2 = 4, 1 + 5 = 6 and 1 + 6 = 7 and same coloured sums are not allowed.
Challenge
For 1 colour, let’s say red, we can only count up to the number 1 like this:
1
For 2 colours, let’s say red and blue, we can count up to 4 like this:
1 2 3 4
Can you explain why we can’t add the number 5?
What is the highest number you can count to using 3 colours?
You can check solutions here:
Here is a python program that generates all the solutions:
https://www.programiz.com/online-compiler/2S5O1C7J96Ys7
See here for the printable puzzle with further explanations and here for a video including the solutions (that are known so far …).
University of Southampton are running a National Cipher Challenge.
Introduction to some of the ciphers that will be used is here.
Competition is https://www.cipherchallenge.org/
There is a great set of tools to use:
https://www.cipherchallenge.org/tools/
Please sign up for the challenge!
Contact Mrs Fleming on [email protected] if you need the monitoring pin to complete the registration.

Here is a series of puzzles with red and blue hats that will challenge your logical skills.
Today we did one of our favourite puzzles inspired by this Numberphile video by Neil Sloane.
Starting with 2 ones, what is the maximum number you can place on an infinite grid according to the rule:
“You can place a number if all the numbers immediately around it add up to itself”
Here is a way to get up to 4:
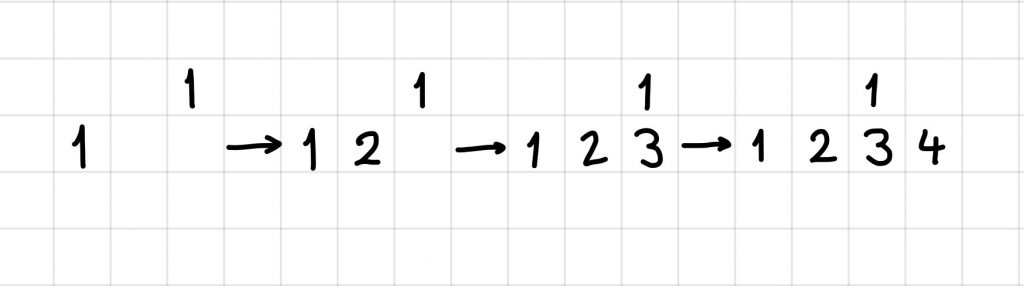
But then we are stuck as there is nowhere to put the 5. Can you do better than 4?
You can choose where to place the 2 ones to start with, for example:


This puzzle can be tried with any number of 1s to start with.
What is the maximum number you can place starting with three 1s?
Some solutions are here.

This investigation is based on the ancient Greek Apollonius Problem: Can you draw a circle that just touches three given circles? How many can you draw?
We tried this by hand and then on Geogebra following these instructions.
The maximum number of circles possible was unsolved for more than 2000 years, but we solved it! For the solutions and more see the links below:

Thanks to Barasa in Kenya for telling us about this one …
Challenge 1
Take 10 cards from a deck – A,2,3, … 10. Ace represents 1.
Arrange the cards in a pile face down so that when you show the first card it is the Ace. Remove this card. Then count to two putting the first card on the bottom of the pile. The second card should be the two. Show it and remove it. Then count to three, each time you say a number you should be putting a card on the bottom and then when you get to 3 you show the 3 and remove it from the pile.
Arrange the cards so that this works for every number from A to 10. By the time you get to 9 you should only have two cards left in your hand! Cycle through them counting 1, 2, 3, … 9 and show the 9. And then you just have 10 left and the trick is over.
Challenge 2
Try to arrange the cards to perform the same trick except you don’t remove the card when you show it. The card is just placed at the bottom of the pile and you start counting the next number.
You should find out that this is impossible for 10 cards. Is there a number of cards that it would work for?
We tried a dice puzzle today set a while back by Matt Parker.
You only have the tool above – three dice inside a cube.
But you want to play a game that requires throwing a single dice and then a game that requires throwing two dice and adding their score together. Is there a way that you can use the sum of these three dice to simulate both of these scenarios?
Task 1
First work out the distribution of numbers you can score with three dice
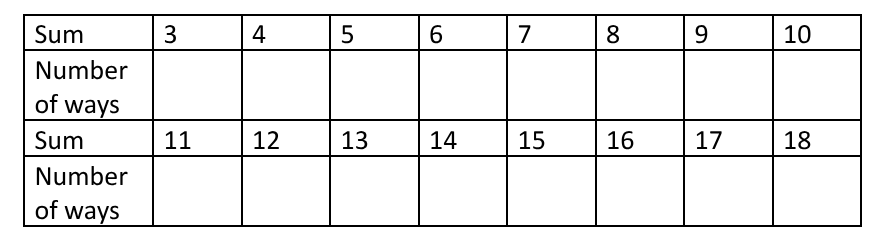
Can you map this in a nice way to the distribution for 1 dice?
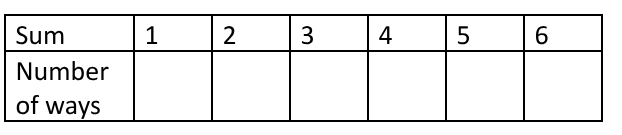
Task 2
How about for 2 dice?

Might not be able to do it using (only) the sum …
Printable worksheet here.
Succinct solution here or watch the full brilliant video by Matt.

Today we worked on an absorbing puzzle that you can play online here:
https://www.cleverlearning.co.uk/blogs/blogConwayInteractive.php