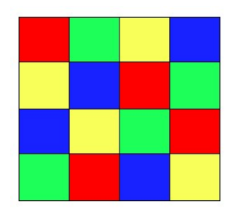
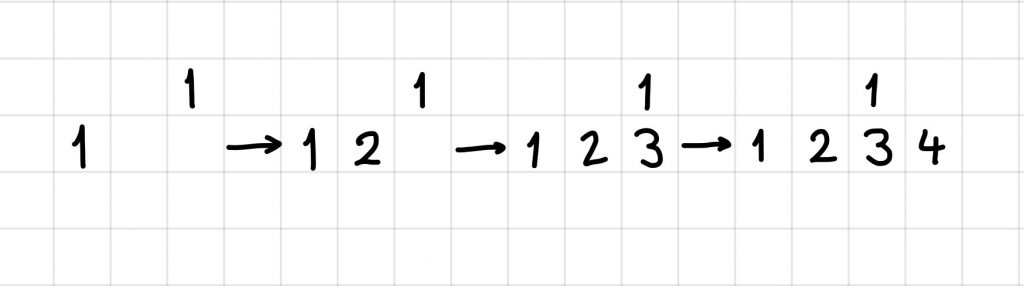
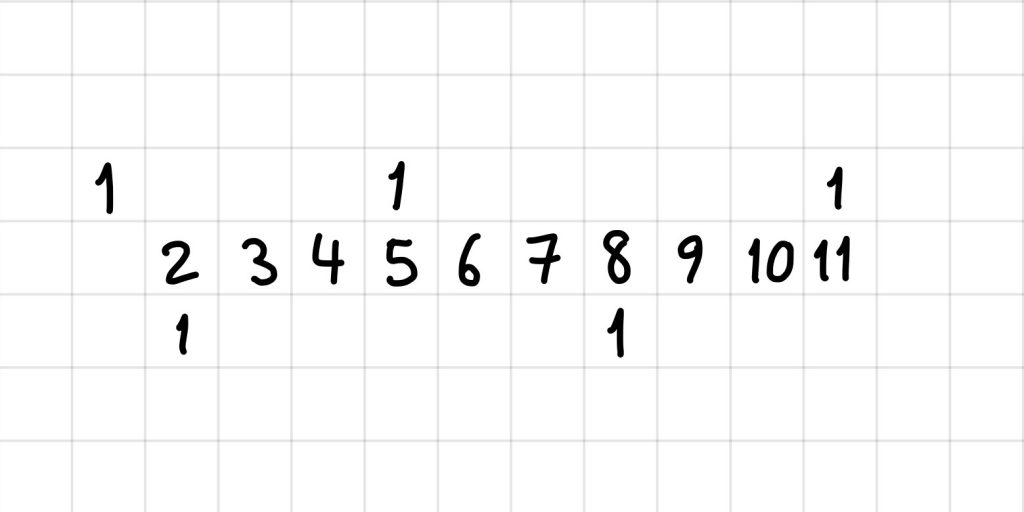This highly addictive shape game is brilliant fun and has some interesting mathematical ideas to explore. We started with drawing all the one block, two block, three block and four block shapes we could think of. No repeats (reflections, rotations) were allowed – for example these two shapes of four blocks are effectively the same:


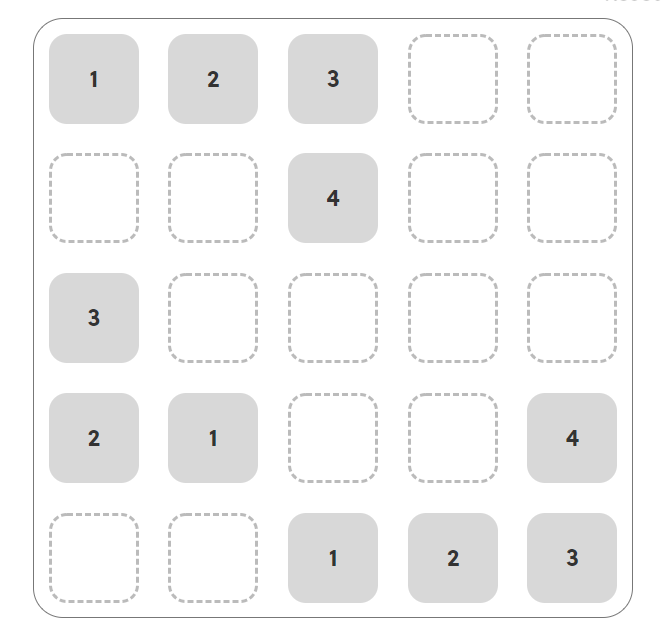
There are 9 different shapes, and the game contains each of these possibilities. There are 7 dice which you throw to generate where to put 7 wooden pieces. For example the game could start like this:
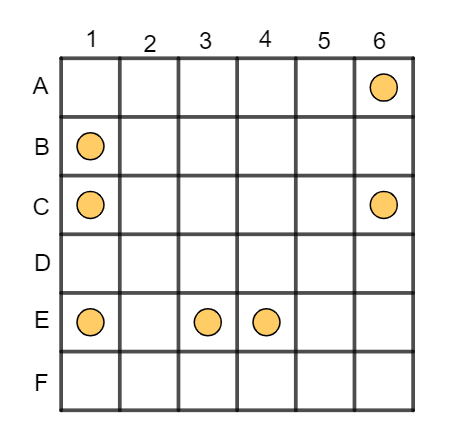
The values on the dice are:

Once you have the wooden pieces in place, it is a two player race to fit all the coloured pieces on the grid. Given the dice configuration above, how many possible games are there to play? The makers of the game have ensured all these games are possible in at least one way.
After we played a few times, we tried to make up an impossible configuration of wooden pieces (ignoring the dice). Here is a trivially impossible one (because there is only one blue one block piece):

But can you make up one that looks like it could work but then doesn’t? Ghazi even found a way of generating impossible solutions and proving they were impossible.