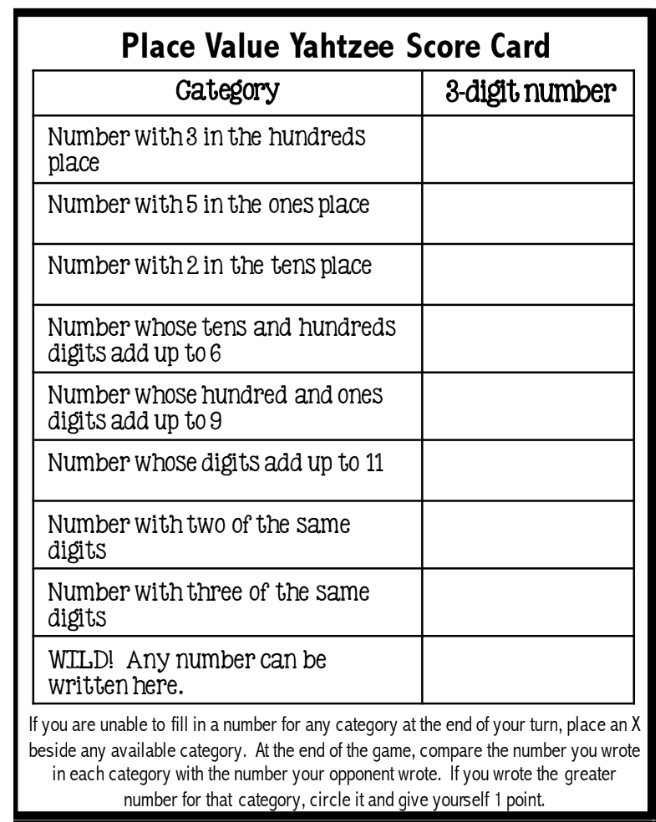
For our final maths club session of the year we played a fun version of Yahtzee from this great website called Games4Gains.

For our final maths club session of the year we played a fun version of Yahtzee from this great website called Games4Gains.
We looked at Math Pickle’s brilliant activity. Finishing up with working out this probability:
This activity was inspired by this numberphile video by Neil Sloane.
Here are the only distinct three ways you can draw two circles in a Venn diagram.
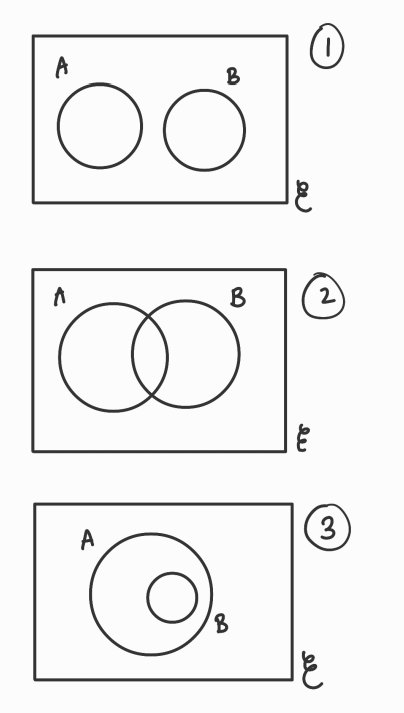
If we take the universal set to be the positive integers, we can come up with some sets that would fit for A and B for the three examples.
Note that these choices mean that there is at least one number in each region.
Now for the challenge …
Draw all the different Venn diagrams you can make with three circles, and find rules for them all.
Number of ways can be found here. A picture of them all is here.
Watch the numberphile video to find out how many Jonathan Wild found for 4 and 5 circles. It is a lot more! Nobody knows for 6 …

We spent today learning about infinity and Hilbert’s Infinite Hotel:
You might be familiar with divisibility rules such as “A number is divisible by 3 if the sum of the digits is divisible by 3”. You can see some more here.
Our investigation today was – can we develop a set of divisibility rules for binary numbers?
Divisible by 2
This was straightforward. If the rightmost (unit) digit is 0 then the number is divisible by 2.
e.g. The number 6 is divisible by 2
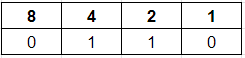
but the number 7 is not
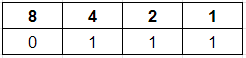
Can you extend this logic to create a divisibility rule for powers of 2 (e.g. 4, 8, 16 …)? Solution
This activity came from watching this Numberphile video . A worksheet of the activities below is available here.
Suppose that we want to colour the whole plane so that any two points at distance 1 from each other would have different colors.
You can imagine this as walking on a tiled floor in jumps of 1 and each jump has to be onto a different colour.
What is the minimum number of colours we would need to use?
Finding an upper bound to the number of colours needed
Task 1
It doesn’t have to be a regular tiling, but would 4 colours work if we coloured the plane like above? How big would the squares have to be?
Task 2
Find a number of colours that would work for a square tiling. How big would the squares have to be?
Task 3
Show that we would need at most 7 colours using a different shape tile (isometric paper will be helpful!).
Finding an lower bound to the number of colours needed
Task 4
Use this diagram to show that we would need at least 3 colours to colour the plane.
Task 5
Create a graph of points to show that we need at least 4 colours.
Further reading
This problem is called the Hadwiger–Nelson problem and was stated in 1950. It was recently (2018!) proved that you need at least 5 colours by an amaetur mathematician who was working on it as a break from his job as a maverick biologist intent on extending the human lifespan! The middle dot in the picture below has to be white rather than red, green, blue or yellow like the rest. It is still an open problem to find the smallest number of colors. It could now be 5, 6 or 7 and nobody knows.
Links:
https://www.quantamagazine.org/decades-old-graph-problem-yields-to-amateur-mathematician-20180417/
https://www.theguardian.com/science/2018/may/04/60-year-old-maths-problem-partly-solved-by-amateur
https://mathworld.wolfram.com/Hadwiger-NelsonProblem.html
Today we used inspiration from Nrich and mathsisfun.com to explore the Platonic solids on Polypad.

Go to https://polypad.amplify.com/p#polygons and make a net of a dodecahedron. You can keep adding pentagons together and then highlight them all and click Fold Net.
If it is not quite right, click Unfold Net and then add/remove pentagons and try again.
The angle deficit at a vertex of a polyhedron is a measure of how far short each angle sum is from 360°. For example, in a dodecahedron, three pentagons with interior angles of 108° meet at each vertex, so the angle sum is 324° and the angle deficit is 36°:
The total angle deficit is the sum of the deficits at each vertex.
Can you fill in the table for the Dodecahedron:
Platonic Solids
| Regular polygons | Faces | Vertex form | Angle Sum | Angle Deficit | Number of Vertices | Total Angle Deficit | |
| Cube | Squares | ||||||
| Tetrahedron | Triangle | ||||||
| Octahedron | Triangle | ||||||
| Icosahedron | Triangle | ||||||
| Dodecahedron | Pentagon | 5,5,5 | 324 | 36 |
Task 3 – Make the nets and fill in the table for the other four Platonic Solids. These are 3D shapes where the faces are congruent regular polygons and the same number of faces meet at each vertex.
Task 4 – Find all the Archimedean Solids which are formed by two or more types of regular polygons, each with the same side length and such that each vertex has the same pattern of polygons around it.
Further reading
https://polypad.amplify.com/lesson/five-platonic-solids
https://www.maths.ed.ac.uk/sites/default/files/atoms/files/platonic_solids_reduced.pdf
We tried this fun game today in maths club and then started to code it. See this previous post for similar code to adapt.
Breaking news!!!! You can now do python on Geogebra. Try it out here. And here is an article about it.
Could you adapt the program above to make a nice tesselation of hexagons?
Or you could try squares to start with? Here is a solution for squares.
Also check out the examples on the site by going to File – Open – Examples