Student versions of todays puzzle: English Français
Facilitator versions of todays puzzle: English Français
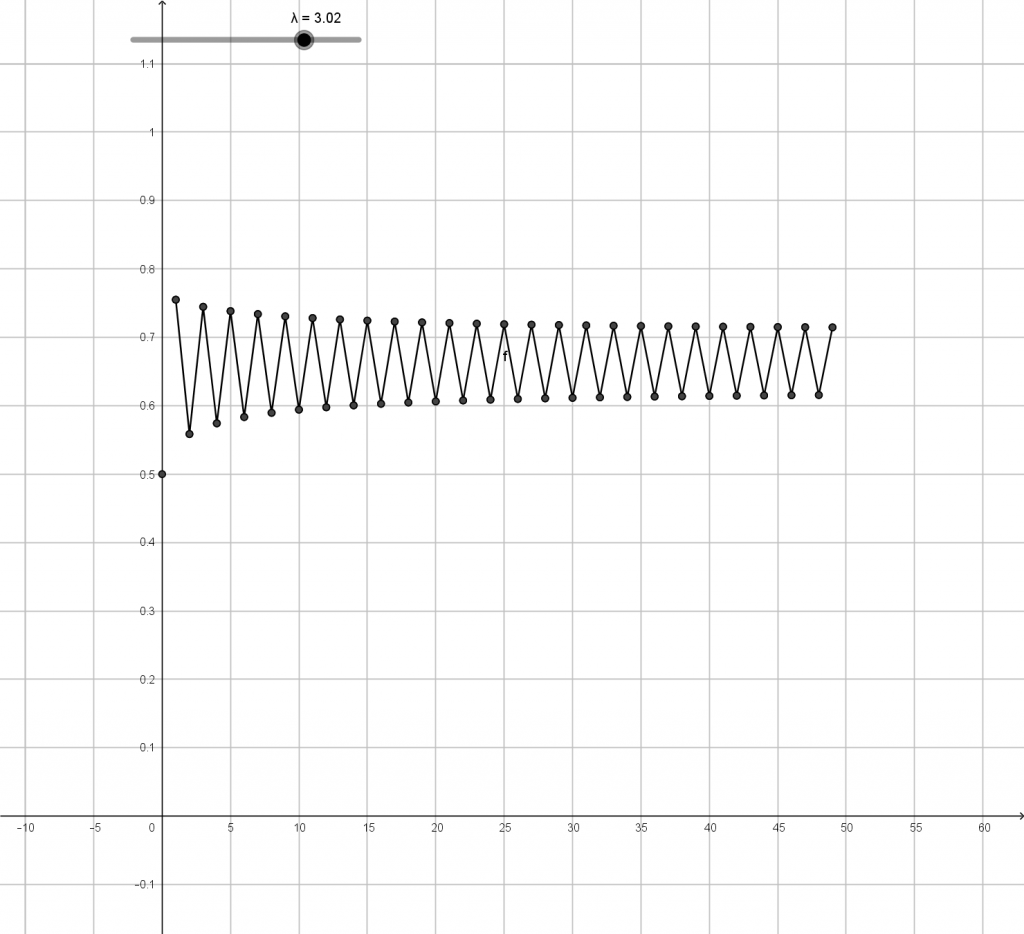
Konstantin Oskolkov of the Steklov Mathematical Institute in Moscow was told about this puzzle by a stranger c.1980. It has become known as Bulgarian Solitaire. It has been written up by MathPickle in terms of King Kong here.