
Try out the game here.
Can you adapt the Mastermind code below to make the game above?
Starting with the following trinket can you draw a simple square and hexagon?
Can you write a program that asks for the number of sides, and dependent on your answer, produces a drawing like this:

By following a simple iterative formula and using complex numbers, the fantastic shape above can be created. Some starting instructions are here.
Today we played a geometric game and tried to solve a couple of maths questions around it. See here for more details.

We played a “perfect strategy” game today where everyone theoretically has an equal chance of winning.
The game is called 91 and the rules are below.
We also played a couple of “collaborative games” where all players work together to try and beat the cards. The two we played were German games called The Game and Hanabi.
Rules for 91:
Number of players: 2-7
Materials: 1 card deck for 2-3 players; 2 card decks for 4-7 players (no jokers).
Players and Cards: The game is for two to seven players, using a complete suit from a standard 52-card pack for each player plus one extra suit. Two decks are needed for four or more players. Cards rank Ace (low), 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K (high). As a prize, the Ace is worth 1 point, cards 2-10 face value, Jack 11, Queen 12 and King 13.
Setup: The cards are sorted into suits. One suit (traditionally diamonds) is shuffled and stacked face down as a prize pile. Each of the other players takes one complete suit.
Play: The top card of the prize pile is turned face up (so you see its value). Then each player selects a card from their hand with which to bid for it and places it face down (so you can’t see its value). When all players are ready, the bid cards are revealed simultaneously, and the highest bid wins the prize card. The bid cards are then discarded and the prize card is placed beside the player who won it. The next card of the prize pile is turned face up and players bid for it in the same way. If two players put the highest bit, the bid cards are discarded but the prize card remains on offer. A new prize card is turned face up and all players then make their next bid for the two prize cards together, then for three prize cards if there is another tie, and so on. If any of the players’ last bid cards are equal, the last prize card (and any others remaining from immediately preceding tied bids) are not won by any player.
Scoring: When all players run out of bid cards, the play ends. Each player totals the value of the diamonds they have won in bids (Ace=1, 2- 10 face value, J=11, Q=12, K=13) and the greater total wins the game.
We ran through a whole series of puzzles today starting with the obvious and getting into some challenging maths.
The general concept was trying to guess what hat you are wearing based on info you can see of those around you and on a careful strategies decided on beforehand. You can see the list of challenges here.
Today we played a game where everyone simultaneously guesses a number between 0 and 100. The person who is closest to the average (mean) wins. What number would you choose?
The game is played in multiple rounds. It is interesting to see how strategies change and how the mean changes over time.
One fun variation is that the winner is the person who is closed to 2/3 of the mean – an analysis is here.
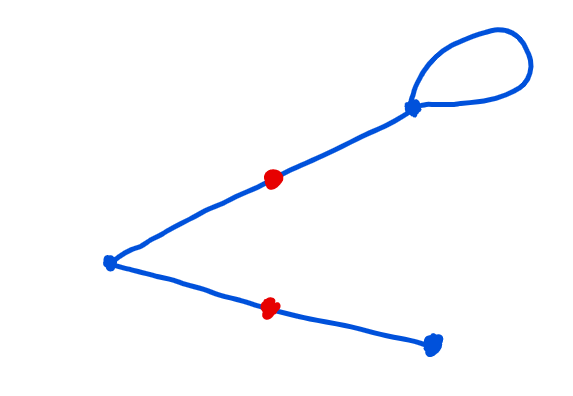
We played a game that John H. Conway he co-invented with Michael S. Paterson while they were both at Cambridge.
It is called Sprouts, and the rules are summarised by Nrich here.
You can try and discover some of the maths behind it by working through this article. We managed to prove the maximum and minimum number of moves for a game starting with three points.
We started with this warm up puzzle from Nrich:
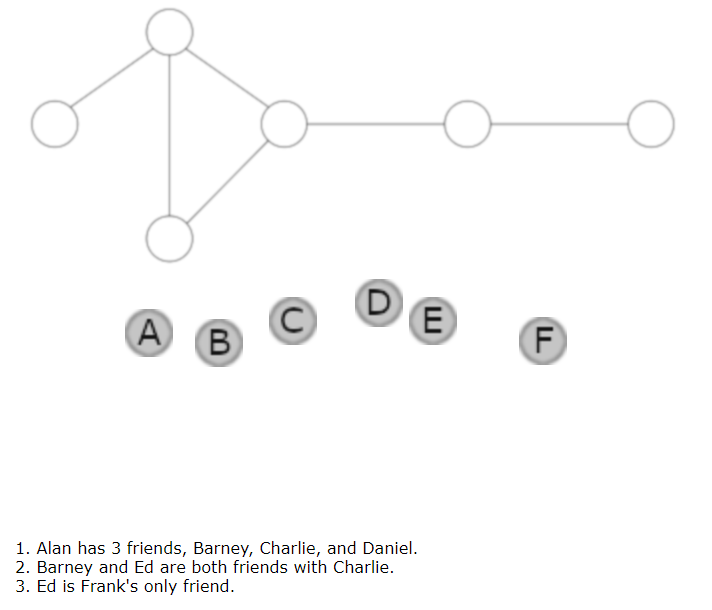
The interactive version is here.
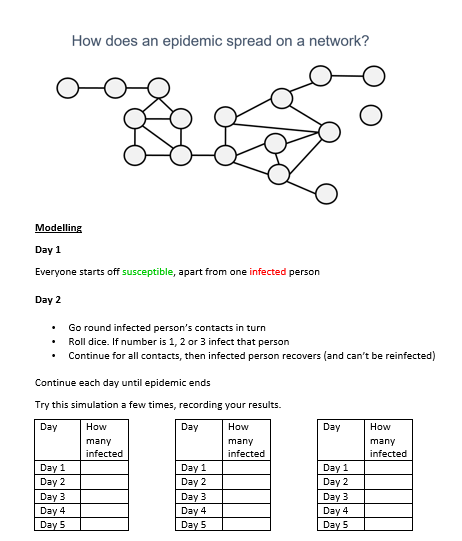
We then used this worksheet to explore how a disease could spread through a network. This was adapted from this set of resources from Nrich.
Take 7 playing cards.
Put them into any number of piles and arrange in descending order. For example:

Take one card from each pile to form a new pile.
Put the piles in descending order.
Keep repeating this process.
What do you notice?
Try all different combinations of 7 cards and try and represent your findings on paper. What is the longest sequence you can find?
Then try with 6 cards. What is different this time?
For more questions and solutions see our SAMI Maths Club app.