
We did this brilliant activity from Think Maths and Matt Parker using dice and excel

We did this brilliant activity from Think Maths and Matt Parker using dice and excel
Practical Numbers

This activity was inspired by this numberphile video.
20 is a practical number because it could be used to design a set of weights where all of its factors are the weights and you can weigh all the numbers from 1 to 20 using each weight only once.
The factors of 20 are: 1, 2, 4, 5, 10 and 20
And you can make the numbers 1 to 20 using combinations of these numbers (each number can be used a maximum of once):
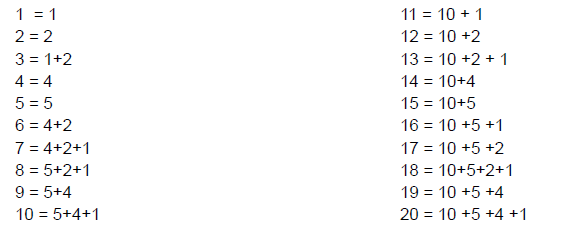
So 20 is a practical number
Of course all powers of 2 are practical numbers, but can you find some others?
Do they have anything in common?
Are there an infinite number of practical numbers?
Once you’ve found some can you use them to generate more?
Using these facts:
So for example with the primitive practical numbers 1 and 2 you can generate 2*2=4
So 4 is not a primitive number as it can be generated from previous ones.
Can you circle all the practical numbers in this grid, using a different colour for primitive practical numbers?
Solution can be found here. To read more about Practical Numbers check out Wikipedia and this talk.
Using Python
Task 1
https://trinket.io/python/c9f4762222
Change the program so that the factors are given in a list (you can use e.g. factors.append(i) after setting up a blank list called factors
Task 2 – change the program so that instead of asking the user for a number it displays the factors of all the numbers from 1 to 30.
Task 3
totals=[]
factors=[“a”,”b”,”c”,”d”]
Write a program that starts as above and prints this:
[‘a’, ‘b’, ‘c’, ‘d’, ‘ab’, ‘ac’, ‘ad’, ‘bc’, ‘bd’, ‘cd’, ‘abc’, ‘abd’, ‘acd’, ‘bcd’, ‘abcd’]
This is a starting point if you are stuck.
Task 4
Adapt your program for Task 3 to work with any factor list up to 7
Solution to Task 4 up to length 7
Chatgpt solution for any length!
Task 5
Combine your programs from Task 2 and Task 4 to list all the totals that can be made with the factors of numbers from 1 and 30.
It should display like this:
The factors of 1 are:
[1]
and all the totals you can make are:
[1]
The factors of 2 are:
[1, 2]
and all the totals you can make are:
[1, 2, 3]
The factors of 3 are:
[1, 3]
and all the totals you can make are:
[1, 3, 4]
The factors of 4 are:
[1, 2, 4]
and all the totals you can make are:
[1, 2, 4, 3, 5, 6, 7]
You can use this code to print a new line:
print(“\n”)
Task 6
Find all the practical numbers between 1 and 30
Task 7
Watch this numberphile video!
Task 8
After watching the video can you think of some improvements to make your code more efficient?
Start with this Nrich activity:
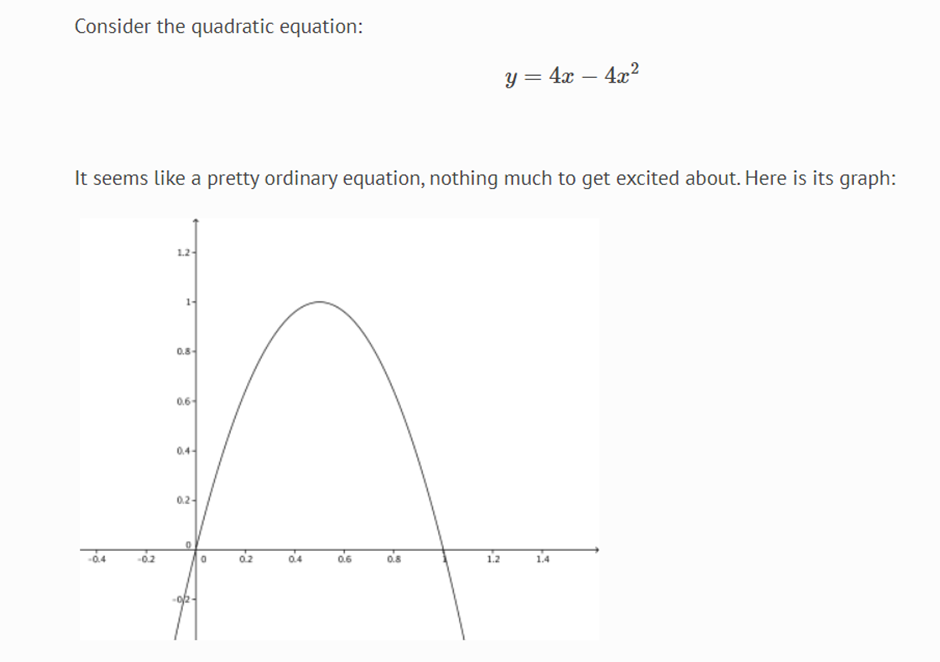
Use your calculator to plug in some numbers. Start with a value for x, say x=0.2, apply your equation and get y=0.64.
Now try again, this time using this new value for x: plug in x=0.64 and get y=0.9216.
Go again, with the new value x=0.9216 and get y=0.28901376.
Carry on repeating this process (called iterating) for as long as takes your fancy, and you’ll get a sequence of numbers:
0.2, 0.64, 0.9216, 0.28901376, ________________, ________________, ________________
What do you think would have happened if you had started this process with a value of 0.2001 for x rather than 0.2? Those two numbers are very close, almost the same, so you would think they’d produce a fairly similar sequence of numbers…
____,____,_________,_____________, ________________, ________________, ________________
Try this on a spreadsheet and graph your two sequences (against sequence number). What do you notice?
Then watch https://www.youtube.com/watch?v=6z4qRhpBIyA Then try and recreate it using the code below as a starting point.
Read here about the discovery of chaos theory.
A pdf of this activity is here.
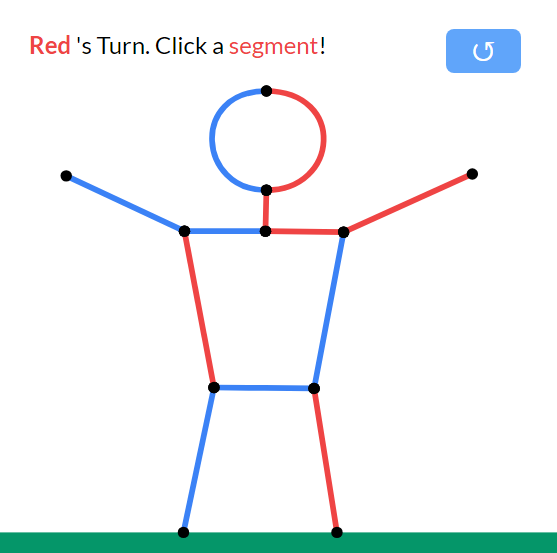
This fun two player game has a lot of strategies to consider …
The rules (from Wikipedia) are
Each line segment is coloured either red or blue. One player (usually the first, or left, player) is only allowed to cut blue line segments, while the other player (usually the second, or right, player) is only allowed to cut red line segments.
On their turn, a player “cuts” (erases) any line segment of their choice. Every line segment no longer connected to the ground by any path “falls” (i.e., gets erased). According to the normal play convention of combinatorial game theory, the first player who is unable to move loses.
Try it out here.
Can you create your own starting grids so that …
Player blue wins, regardless of if they go first or second
Player 1 wins, regardless of if they are red or blue
Player 2 wins, regardless of if they are red or blue
They might not all be possible!
Lots more to read here.
It is also interesting to analyse the “game value”, for example:
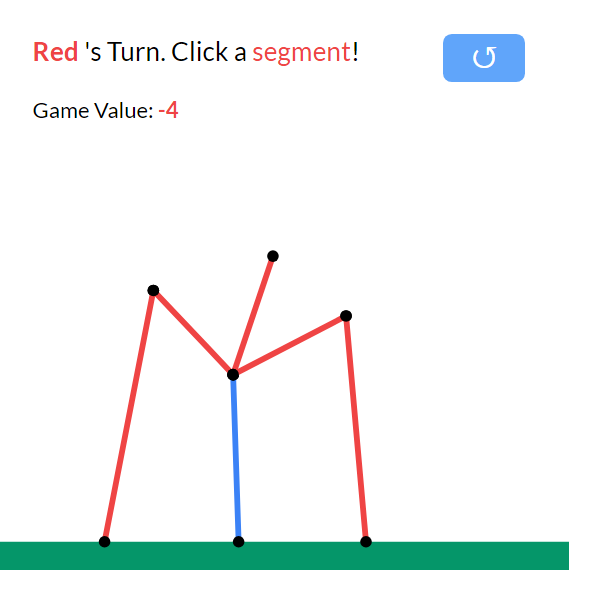
For some ideas on how to calculate the game value see this exploration.
We worked on ideas from this NRich activity today.
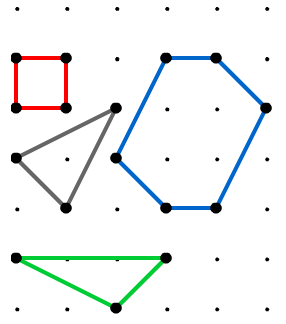
When the dots on square dotty paper are joined by straight lines the enclosed figures have dots on their perimeter (a) and often internal (b) ones as well.
Figures can be described in this way: (a,b).
For example, the red square has an (a,b) of (4,0), the grey triangle (3,1), the green triangle (5,0) and the blue hexagon (6,4):
Questions:
Here are our solutions.
For more info on this theorem see the solutions in the Nrich activity and watch this brilliant proof.

We played the great game of SET and then answered these questions. The answers can be found in this document from The Madison Math Circle. Thanks to them and David J Bruce for the ideas.
We also started to think about how to represent cards in a geometric space. If you take a simple game of set with just two characteristics, you can plot each card in 2D and hence work out how many cards you can have on the table before you make a set (by not drawing a straight line). See here for the details.
The Irish logarithm is an algorithm invented by Percy Ludgate in 1909 for multiplying single-digit numbers. The idea was to program a computer to do these calculations.
The algorithm uses two tables to perform the multiplication. With just these tables you can calculate products up to 9×9 simply by adding two numbers together.
Here are blank versions of the two tables below (and as a pdf).

Our challenge was to fill in these tables. Here is the start of an attempt that would not work …
1 x 2 would be 1+2 so the correct answer of 2 needs to be in the box called 3.
1×3 would be 1+3 so the correct answer of 3 needs to be in the box called 4.
2×3 would be 2+3 so the correct answer of 6 needs to be in the box called 5.
So far so good ….
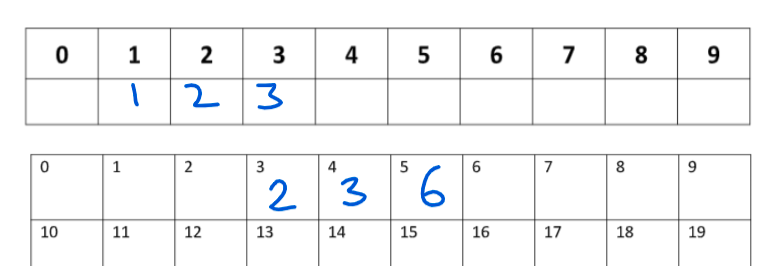
But … 2×2 would be 2+2 so the correct answer of 4 needs to go in the box called 4. But the box called 4 already has a 3 in it, so our initial choice of numbers is a bad one.
Can you do better?
It is very difficult to come up with the solution from scratch (but do try!). Here are a few numbers already filled in, if you would like a starting point (and as a pdf).
The solution is not unique, but here is Ludgate’s solution (and as a pdf).
This activity was created using content from this worksheet from Maths Craft NZ and this Mathigon Tesselation Activity.
A tiling consists of covering a surface (a plane) using copies of shapes, called tiles, without overlapping or leaving gaps.
For example if we use a square or an equilateral triangle as a tile we can create a tiling that will cover an infinite plane.

Only one other regular (all sides and angles the same) polygon can tile the plane, which polygon is this?
Can you prove that there are no others?
You can also use multiple shapes to tile the plane. For example:

You can also use irregular shapes to tile the plane, any triangle or quadrilateral works:

Exactly 15 different pentagons will work, for example:

Go to Mathigon and make a tiling using either one regular polygon, one irregular triangle or quadrilateral or multiple shapes. Use the “Polygons and Shapes” or Pentagon Tilings” menus. You can change colour at the bottom.
All the above tilings are periodic tilings which means they have translational symmetry.
Go to Mathigon and make a tiling using either one regular polygon, one irregular polygon or multiple shapes.Use the “Polygons and Shapes” or Pentagon Tilings” menus. You can change the colour of the tiles at the bottom and you can quickly duplicate whole sections of your tiling by highlighting and clicking on the copy icon.
All the above tilings are periodic tilings which means they have translational symmetry.
From wikipedia:
Covering a flat surface (“the plane”) with some pattern of geometric shapes (“tiles”), with no overlaps or gaps, is called a tiling. The most familiar tilings, such as covering a floor with squares meeting edge-to-edge, are examples of periodic tilings. If a square tiling is shifted by the width of a tile, parallel to the sides of the tile, the result is the same pattern of tiles as before the shift. A shift (formally, a translation) that preserves the tiling in this way is called a period of the tiling. A tiling is called periodic when it has periods that shift the tiling in two different directions.
The tiles in the square tiling have only one shape, and it is common for other tilings to have only a finite number of shapes. These shapes are called prototiles, and a set of prototiles is said to admit a tiling or tile the plane if there is a tiling of the plane using only these shapes. That is, each tile in the tiling must be congruent to one of these prototiles.
A tiling that has no periods is non-periodic. A set of prototiles is said to be aperiodic if all of its tilings are non-periodic, and in this case its tilings are also called aperiodic tilings.
In 1961 Robert Berger constructed such a set, using more than 20,406 tiles. Later he found a much smaller set of 104, and Donald Knuth was able to reduce the number to 92.
Then Raphael M. Robinson found this set of 6 tiles in 1971:
In the mid 70s Roger Penrose found a two tile set that would work. This discovery eventually led to him suing a toilet paper company and to a new way to make non stick frying pans.
And finally in 2022 a retired systems printing engineer found a single tile – called an Einstein tile for the German for one stone.
A Penrose tiling uses only two shapes, with rules on how they are allowed to go together. These shapes are called kites and darts and in the mathigon version they have white lines that need to match up. This means for example that the dart cannot sit on the kite. Three possible ways to start a Penrose tiling are:
These are called the ‘star’, ‘sun’ and ‘ace’ respectively.
Using the pictures above, can you calculate all the angles in the dart and the kite?
There are 4 other ways to arrange the tiles around a point. Can you find them all?
The solution is here
Oxford Online Maths club have done a nice video on this topic. Roger Penrose is a famous professor at Oxford and has a floor built in his honour with his tiles:
Here is an editable version of this page.
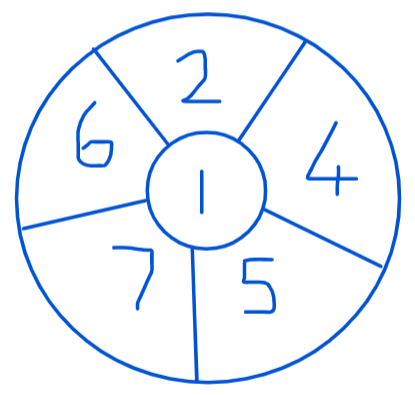
We found this activity on Nrich and it was originally in one of Brian Bolt’s books and developed by MEDIAN in their collection of interesting number resources.
This Daisy is special because you can make every number from 1 to 25.
You are only allowed to add neighbours (numbers touching each other) and you can
only use each number once in a sum.
1 = 1
2 = 2
3 = 1 + 2
4 = 4
5 = 5
6 = 2 + 4
7 = 1 + 2 + 4
8 = 5 + 1 + 2
9 = 4 + 5
10 = 7 + 1 + 2
11 = 5 + 4 + 2
12 = 5 + 4 + 2 + 1
13 = 7 + 6
14 = 7 + 6 + 1
15 = 7 + 6 + 2
16 = 7 + 6 + 2 + 1
17 = 7 + 5 + 4 + 1
18 = 7 + 5 + 4 + 2
19 = 7 + 5 + 4 + 2 + 1
20 = 5 + 7 + 6 + 2
21 = 5 + 7 + 6 + 2 + 1
22 = 4 + 5 + 7 + 6
23 = 5 + 7 + 6 + 1 + 4
24 = 5 + 7 + 6 + 2 + 4
25 = 5 + 7 + 6 + 2 + 4 + 1
Can you do better than this with a different set of numbers?
The challenge is to find six numbers to go in the Daisy from which you can make all the numbers from 1 to a number bigger than 25.
You can check your ideas here:
Could you adapt the program above to search for a higher solution?
To write the program above we needed to find all the combinations from a general daisy like this:
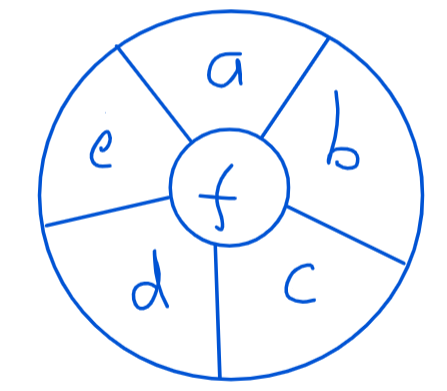
For example you can have a+b or a+f but not a+d. Can you find all the combinations? There is a worksheet to fill in here (with the solution on the second page). An editable version is here.

Today we cracked codes on this site https://www.cipherchallenge.org/ set up by the University of Southampton.
This page is great for decrypting.