Category: Christmas Puzzles Solutions

Here is an example of the experiment we did:

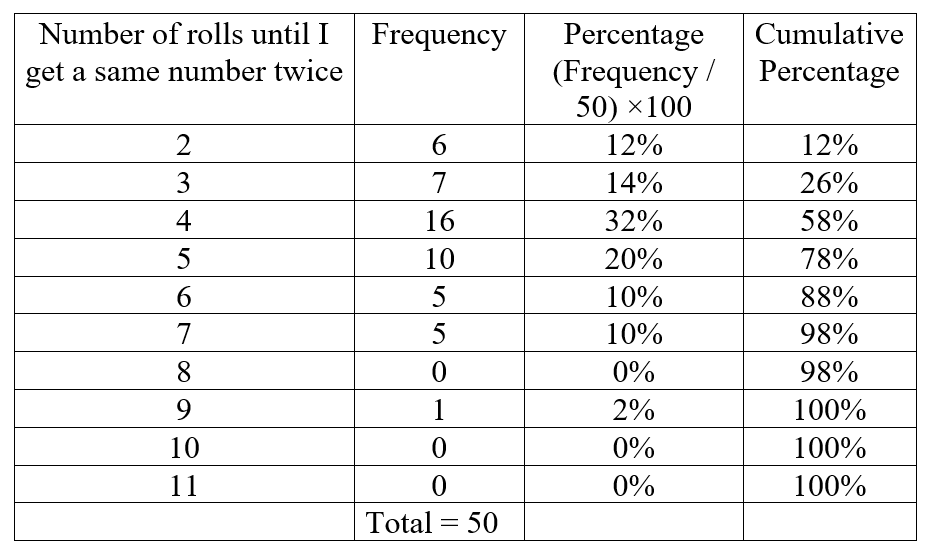
It looks like it only takes 4 rolls to have a 50% chance of getting a double … smaller than you might think! The more trials we do, the more accurate our results. You can run many trials in the applet below:

 

You can also use the applet above to try different number of sides on the dice. How many rolls do you think it would take to have a 50% chance to get a double on a 20 sided dice?

If you extend this question to 365 sides … it is the Birthday Problem! How many people do you have to have in a room for there to be over 50% chance of two people sharing a birthday? Try and discover the answer using the applet above, or see our card deck website for the maths behind the answer.

Take the total amount of presents as x. Santa will be working at a rate of x/60 presents per minute, and Mrs Claus at a rate of x/40 minutes.

By simply adding the rates together,

x/60 + x/40 = 100x/2400 = x/24,

we can find the answer, 24 minutes.

The teacher goes round the circle four times. If there was an even number of children, the sixth child would always receive a blue present and would have four blue presents at the end. Since they only have two blue presents, there must be an odd number of children in the circle.

With the same logic for the green presents the answer can’t be a multiple of 3.

The sixth child receives a green present in the first round because 6 is a multiple of 3. She only receives one more green present so the answer can’t be a multiple of 3.

The options are 7, 11, 13, 17, 19 … and so 7 is the fewest number of children.

The lowest common multiple of 6, 14, and 60 is 420 (7×6×10). So 7 hours after noon.

7pm is the answer.

There must be 4 decorated trees and 5 not decorated.

The first assumption that can be made is that either Penny, Olivia or Noah are lying, because if Penny is lying, everyone else is truthful, and if Matt is lying, Penny states that Noah or Olivia are also lying, so either one of those three are lying, which means there are too many liars.

Therefore, we have two truths: there is one more decorated tree than undecorated, and the number of trees is prime, what Matt says. Starting with all primes smaller than ten, there could be 2 undecorated and 3 decorated trees, 4 undecorated and 5 decorated trees, or 6 undecorated and 7 decorated trees.

If Olivia is telling the truth, the total is 9 (4+5) , which also means that Noah is telling the truth ( 8 < 9 < 12), and Penny is lying. In the other cases, both Noah and Olivia must be lying at once(2+3 < 8 and 6+7 > 12, none of these possibilites contain 4).

The only possible solution is when Penny is lying, and we’ve seen that in this scenario, there are 5 decorated trees and 4 undecorated trees.

You could solve this by simultaneous equations, but there is a quick way to do it without working out how much each present costs.

Add together all the amounts – this will give you double the cost as each colour present appears twice. Then just divide your answer by 2.

(£22+£15+£16+£32+£37)/2 = £61

 

The possibilities are:

(Wins, draws, goals)

Rudolphs: (0, 0, 8) or (0, 1, 3)

Comets: (0, 0, 14) or (0, 1, 9) or (0, 2, 4) or (1, 0, 4)

Vixens: (0, 0, 9) or (0, 1, 4)

 

If there were 3 games, then there would be 30 points

for wins and draws, leaving just 1 point for goals,

so that is not possible, since each team scored in each game.

 

Thus, there were only 2 games,

yielding 20 points for wins and draws, 11 for goals,

which reduces the possibilities to

Rudolphs: (0, 1, 3)

Comets: (0, 2, 4) or (1, 0, 4)

Vixens: (0, 1, 4)

 

Rudolphs had a draw (and maybe a loss).

Comets had 2 draws or a win and no other match.

Vixens had a draw (and maybe a loss)

 

If Comets had 2 draws, then both games were draws,

but that is not possible since total goals was 11, which is odd.

So Comets had a win against one of the others,

and the other game was a draw between the Rudolphs and the Vixens.

 

The score of Rudolphs-Vixens draw then was either 1-1, 2-2, or 3-3

Since Vixens scored more goals than Rudolphs, they

are the ones who lost to Comets, and Rudolphs, only playing once,

scored all 3 goals in that game, equalling Vixens.

Comets scored all 4 of their goals in their only game, where

Vixens scored one additional goal.

 

The results were:

Comets  4, Vixens 1

Rudolphs 3, Vixens 3