Here is a series of puzzles with red and blue hats that will challenge your logical skills.
Hat colours
Month: October 2025
Stones on a chessboard
Today we did one of our favourite puzzles inspired by this Numberphile video by Neil Sloane.
Starting with 2 ones, what is the maximum number you can place on an infinite grid according to the rule:
“You can place a number if all the numbers immediately around it add up to itself”
Here is a way to get up to 4:
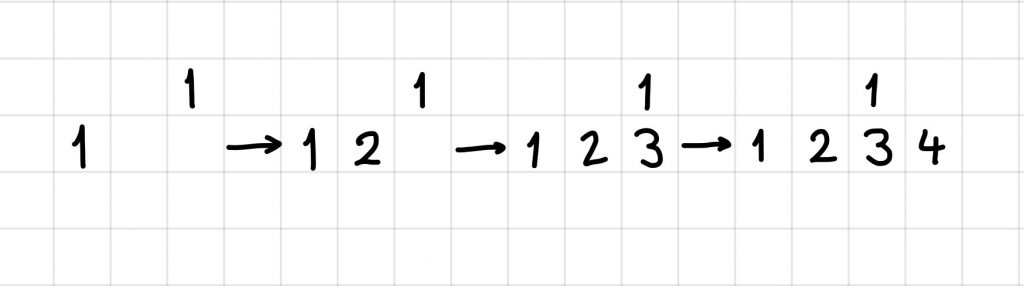
But then we are stuck as there is nowhere to put the 5. Can you do better than 4?
You can choose where to place the 2 ones to start with, for example:
This puzzle can be tried with any number of 1s to start with.
What is the maximum number you can place starting with three 1s?
Some solutions are here.
Apollonius Problem
This investigation is based on the ancient Greek Apollonius Problem: Can you draw a circle that just touches three given circles? How many can you draw?
We tried this by hand and then on Geogebra following these instructions.
The maximum number of circles possible was unsolved for more than 2000 years, but we solved it! For the solutions and more see the links below: