Month: July 2025

We tried a dice puzzle today set a while back by Matt Parker.

You only have the tool above – three dice inside a cube.

But you want to play a game that requires throwing a single dice and then a game that requires throwing two dice and adding their score together. Is there a way that you can use the sum of these three dice to simulate both of these scenarios?

Task 1

First work out the distribution of numbers you can score with three dice

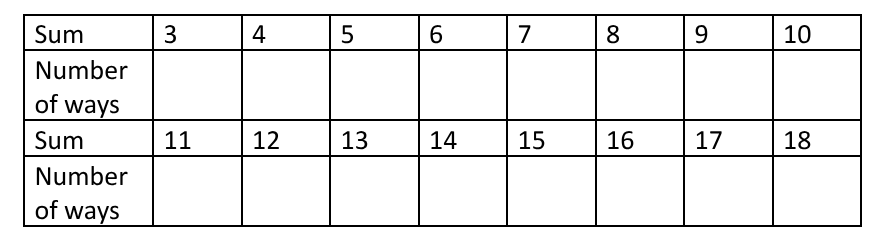
Can you map this in a nice way to the distribution for 1 dice?

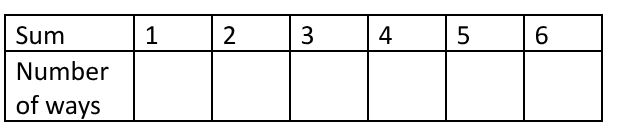
Task 2

How about for 2 dice?

Might not be able to do it using (only) the sum …

Printable worksheet here.

Succinct solution here or watch the full brilliant video by Matt.

Today we worked on an absorbing puzzle that you can play online here:

https://www.cleverlearning.co.uk/blogs/blogConwayInteractive.php

The Irish logarithm is an algorithm invented by Percy Ludgate in 1909 for multiplying single-digit numbers. The idea was to program a computer to do these calculations.
The algorithm uses two tables to perform the multiplication. With just these tables you can calculate products up to 9×9 simply by adding two numbers together.

Here are blank versions of the two tables below (and as a pdf).

Our challenge was to fill in these tables. Here is the start of an attempt that would not work …

1 x 2 would be 1+2 so the correct answer of 2 needs to be in the box called 3.

1×3 would be 1+3 so the correct answer of 3 needs to be in the box called 4.

2×3 would be 2+3 so the correct answer of 6 needs to be in the box called 5.

So far so good ….

But … 2×2 would be 2+2 so the correct answer of 4 needs to go in the box called 4. But the box called 4 already has a 3 in it, so our initial choice of numbers is a bad one.

Can you do better?

It is very difficult to come up with the solution from scratch (but do try!). Here are a few numbers already filled in, if you would like a starting point (and as a pdf).

The solution is not unique, but here is Ludgate’s solution (and as a pdf).