Today we were inspired by this amazing video from 3 Blue 1 Brown.
Can you always draw a rectangle on any shape? How about a square?
Here is a series of challenges on paper and geogebra to explore this fascinating topic.
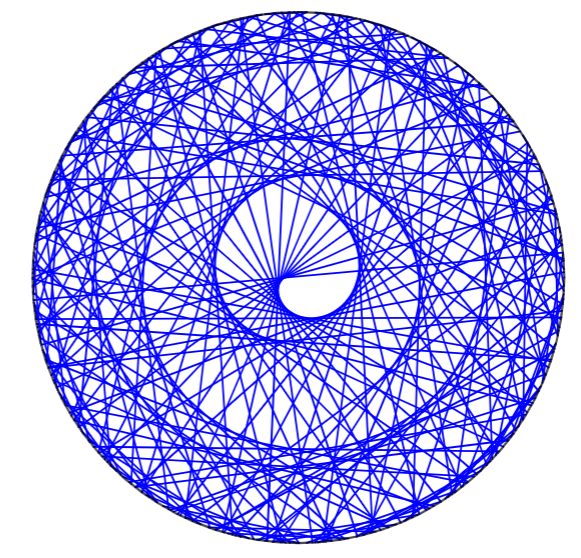
Here are the 1st and 2nd explorations we did today to learn about modular arithmetic and a fantastic geogebra app.
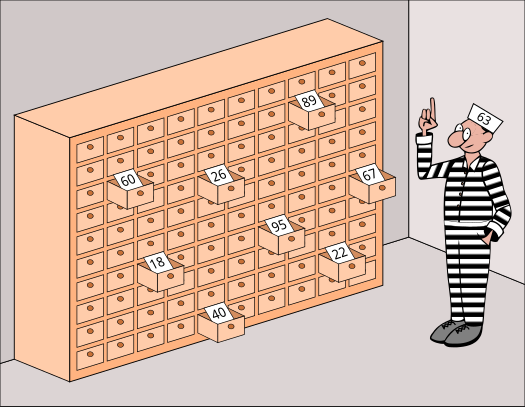
From Wikipedia:
“The 100 prisoners problem is a mathematical problem in probability theory and combinatorics. In this problem, 100 numbered prisoners must find their own numbers in one of 100 drawers in order to survive. The rules state that each prisoner may open only 50 drawers and cannot communicate with other prisoners after the first prisoner enters to look in the drawers. At first glance, the situation appears hopeless, but a clever strategy offers the prisoners a realistic chance of survival.
Anna Gál and Peter Bro Miltersen first proposed the problem in 2003.”
In maths club we tried this problem with just 10 prisoners. You can read about the strategy here.
We analysed the percentage chance of winning by looking at the different possible cycles for 10 prisoners.