Why do we use base 10? How does base 16 work?

Read this brilliant article: https://betterexplained.com/articles/numbers-and-bases/.

Here is a pdf with explanations adapted from Better Explained and all the activities below. Solutions to all the activities can be found here.

Decimal	15	20	32	47	50	170	171	141
Hexadecimal	F	14	20	2F	32	AA	AB	8D

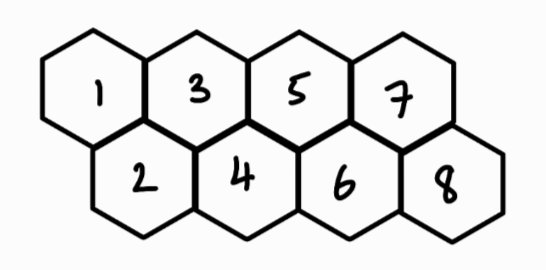
Activity 1

Colour in all the hexagons that are multiples of 7 when converted to decimal numbers.

Activity 2

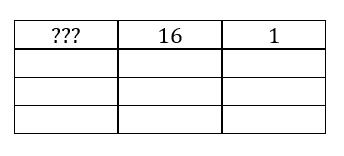
Fill in the table below. You will need to work out what the 3^rd column represents in hexadecimal numbers

Decimal				17	88	740
Hexadecimal	11B	FFF	1000

Activity 3

Find the sum of 3A5 + 2D1 by converting to decimal, doing the addition and converting back to hexadecimal.

Can you do it without converting to decimal numbers?

Activity 4

What’s great about binary?

It’s the simplest number system as it only uses two digits – 1 and 0. This means it is very easy to build in hardware. You just need things that can turn on or off (representing 1 and 0), so it is fundamental to all computers. For example, in a transistor, ‘0’ means no electricity is flowing, whilst ‘1’ means there is a flow of electricity.

How are binary and hexadecimals linked?

Because one block of four binary numbers represents one hexadecimal number it is easy for programmers to visualise numbers in hexadecimal. Programmers sometimes use words written in hexadecimal in their programs.

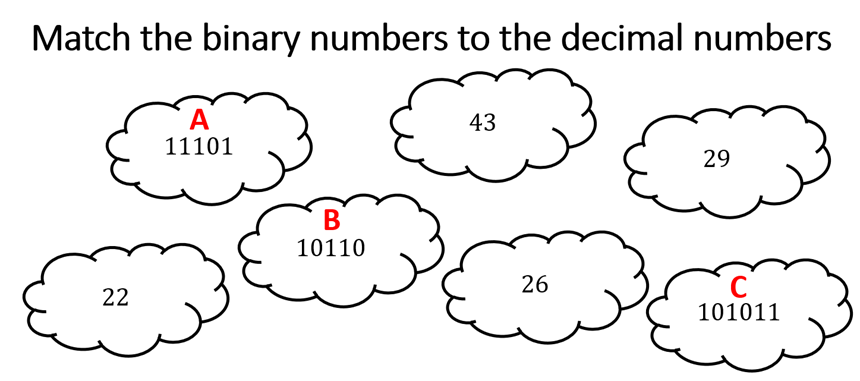
Activity 5

What word is this?

1101 1110 1010 1101 1011 1110 1110 1111

Activity 6

From https://nrich.maths.org/problems/base-puzzle

Find the missing number

10000, ? , 100, 31, 24, 22, 20, 17, 16, 15, 14, 13, 12, 11, 10

Today we played a brilliant game called The Mind where in teams of 2-4 you try to psychically play your cards in ascending order.

We then worked on this code to play collaboratively with a computer working on a perfect timing strategy.

How many different paths are there starting at 1 and finishing at 8 (throught adjacent hexagons only)?

You can only move to a higher number as you go.

We found a number of paths and then looked at a smaller number of hexagons (1,2,3, … etc) until we saw an interesting pattern! Notes/solution here.

A fun related problem can be found here.