Month: January 2020

We were very lucky to have ex Lycee student and maths club attendee Sophia Sergeeva come today to run a session on the Gale-Shapley Stable Marriage Problem. It was absolutely fascinating and delivered brilliantly.

The Problem

This problem looks at matchings: one to one correspondences between sets.

Suppose that we are looking at a strictly heterosexual space (e.g. Tinder) with four boys and four girls. A matching between the boys and girls is sought for. 

Let each of the girls have a list of preferences for the boys (from best to worst) and vice versa.

Let’s name the boys M_A M_B M_C M_D and the girls F_A F_B F_C F_D and list their preferences as follows.

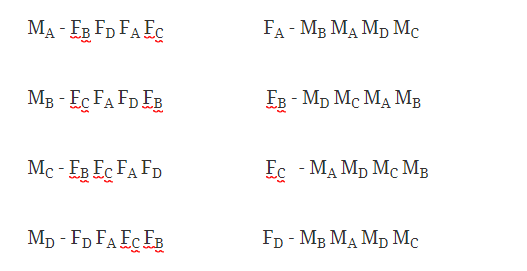
The challenge is to match them up to maximise their happiness such that the system is “stable”. Stable in this sense means that no two people will want to run away together. For example if there exists two couples F₁M₁ and F₂M₂ then if F₁ prefers M₂  to M₁ and M₂ prefers F₁ to F₂  then this is unstable as they will want to run away. Note that it requires both to be true, if there is a couple for which one is top of the list for the other, but the other is bottom then it doesn’t matter as they can’t run away! 

Challenge 1

Find a stable matching for the boys and girls above

The Algorithm

Does a stable matching always exist? Yes, and there is an algorithm to find it. 

In each round of the this first very “traditional” algorithm, each unengaged man proposes to his next favourite woman who hasn’t rejected him. Each woman, if she has one or more suitors, becomes engaged to her favourite suitor and rejects all the others. Rounds continue until men have no one to propose to or are engaged. In subsequent rounds, females can break their engagement if someone they prefer proposes.

In the first stage of this algorithm for our list of preferences, the first round would work like this: 

M_A  – F_B

M_B  – F_C

M_C  – F_B

M_D  – F_D

F_C and F_D have only one suitor so would accept them. F_B has a choice so would choose M_C as he is further up her list of preferences. 

Challenge 2

Carry out the algorithm on the original list to find a stable matching.

Challenge 3

Which group are on average happier in this stable matching, the boys or the girls? Does it make a difference if the females propose? 

Challenge 4

Is there a way that the girls could “lie” in the algorithm to maximise their happiness even if the boys were proposing?!

Challenge 5

Now think of the general case. Does the algorithm always stop? Does it always produce a stable matching? Can you prove it?

Challenge 6

There doesn’t always exist a stable matching for non-hetrosexual preferences. Can you think of a list of preferences of 4 people such that no stable marriage exists? What about 3?

Applications

The Gale-Shapley algorithm is used in real life to solve problems like assigning university places and assigning doctors to hospitals.  Thanks again to Sophia for introducing us to this fascinating problem and algorithm.

We played a brilliant game called Shape Match this week which has been developed by Think Maths – an organisation set up by Matt Parker. There are game cards, shape cards and instructions, but for a quick summary of the rules and the mathematical question we tried to answer, see here. The solution is explained in this document.

Today we played another game from mathemagician Andrew Jeffrey’s great book. Andrew very kindly donated the proceeds of this book to SAMI. 

This game using the cards from Ace (one) up to 9 from a deck of cards.

• The cards are shuffled and each player is dealt 9 cards.
• The players then have to arrange their cards to make a 4-digit number, a 3-digit number and a 2-digit number and put the cards face down on the table.
• Then the players show their numbers and compare them to each other.
• The player with the biggest 2-digit number receives 2 points, the one with the biggest 3-digit number receives 3 points and the one with the biggest 4-digit number receives 4 points. 
• If there’s a tie then the points are split between the players.
• Play five times and see who is the winner …

Can you find a good strategy for this game?

Consider a single player card game with a standard 52 card deck.

You shuffle the cards and turn over the top card.

If you turn over a black card, you win £1. If you turn over a red card, you lose £1.

You can keep turning over cards as long as you want to.

It is impossible to lose money in this game; if you have turned over more red cards than black cards, you can just keep turning over cards until the end of the deck to end up at net £0. If you stop turning over cards before reaching the end of the deck, you keep the money that you have won up until that point.

Is there an optimal strategy for this game?

We played several games of this in maths club just with 10 cards (5 red and 5 black), keeping track of our winnings to start to guess at the best strategy.