Month: February 2018

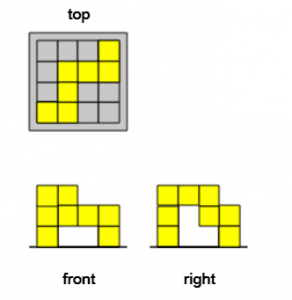
We used this website to solve a series of challenges where you start with front, side and top elevations to build the full picture of 3D shape – building up to using only two views and silhouettes.

In pairs we played the following game a couple of times.

One person is heads (player 1), the other person is tails (player 2). Toss the coin a maximum of 10 times, player 1 gets a point if the coin lands on heads, and player 2 gets a point if the coin lands on tails. If one person becomes three points ahead of the other the game stops and they win. If no one is 3 points ahead after ten tosses the game is a tie.

Which of the following scores are impossible in this game and why? 5-2, 7-4, 6-2

Think of ways the game could end in a tie.

What is the chance of winning this game?

This following table will help.

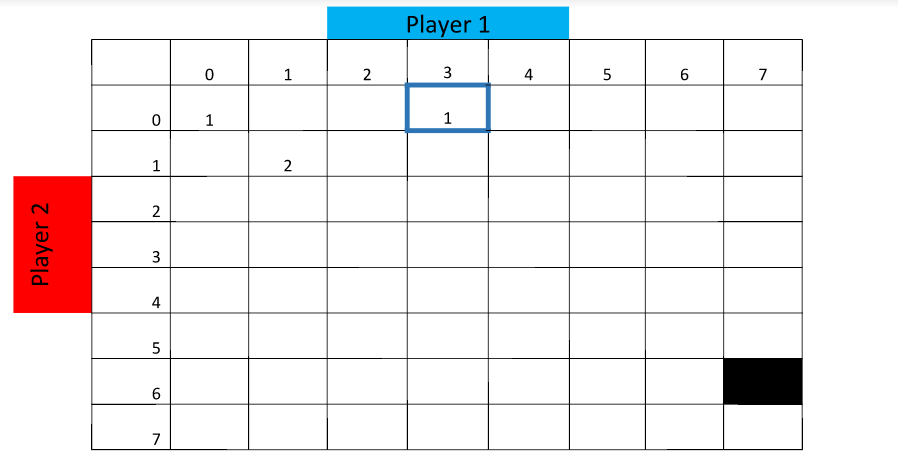
Fill in the table shading out impossible final scores, highlighting winning final scores for Player 1 and Player 2, and highlighting final scores which indicate a draw.
Then write in each box how many ways there are to end up at each score.

A few boxes have been filled in – for example 3-0 is a winning score for player 1, and there is only 1 way to get to that score (1-0 then 2-0 then 3-0). There are two ways to get to a score of 1-1 (0-1 then 1-1 or 1-0 then 1-1). There is a 1 in the 0-0 box as there is just one way to start the game.

See  here for the solution, contained in an excellent presentation by Alex in the Further Maths class in PAL. This puzzle is the starting point for analysing how likely you are to win a tennis match if you only have a one third chance of winning each point. The idea and diagrams in the presentation were taken from the book Game, Set and Math by Ian Stewart.

Unit fractions are fractions that are written in the form ¹⁄_n.

Today’s challenge is to find sums of different unit fractions that are equal to another unit fraction.

For example: ¹⁄₂ = ¹⁄₃ + ¹⁄₆

Let’s see if there is a rule: which of the following are right and which are wrong?

¹⁄₂ = ¹⁄₁₀ + ¹⁄₂₀

¹⁄₃ = ¹⁄₄ + ¹⁄₁₂

¹⁄₃ = ¹⁄₇ + ¹⁄₂₁

¹⁄₄ = ¹⁄₅ + ¹⁄₂₀

The next challenge is to spot the pattern in these sums of unit fractions:

¹⁄₆ = ¹⁄₇ + ¹⁄₄₂

¹⁄₆ = ¹⁄₈ + ¹⁄₂₄

¹⁄₆ = ¹⁄₉ + ¹⁄₁₈

¹⁄₆ = ¹⁄₁₀ + ¹⁄₁₅

Bear in mind that ¹⁄₆ = ¹⁄₁₂ + ¹⁄₁₂ is wrong because both unit fractions are the same.

Try and use this to example to find all the unit fraction sums that add up to ¹⁄₁₈.

What if original fraction is not a unit fraction?

Egyptians had a tendency to write fractions as sums of unit fractions.

Of course, there is an infinite number of ways to do this. Let’s take  for example.

²⁄₃ = ¹⁄₃ + ¹⁄₄ + ¹⁄₁₂

²⁄₃ = ¹⁄₃ + ¹⁄₅ + ¹⁄₂₀ + ¹⁄₁₂

²⁄₃ = ¹⁄₄ + ¹⁄₁₂ + ¹⁄₇ + ¹⁄₄₂ + ¹⁄₃₁ + ¹⁄₉₃₀ + ¹⁄₂₁ + ¹⁄₄₂₀ + ¹⁄₁₃ + ¹⁄₁₅₆

Etc.

But how about expressing non unit fractions as sums of two unit fractions? Here is one example:

²⁄₃ = ¹⁄₂ + ¹⁄₆

But can all fractions with numerator 2 be written as the sum of just 2 unit fractions? Can you prove it?

Let’s finish off with the greedy algorithm. This algorithm, which was developed by Fibonacci, allows you to quickly find a non-unit fraction as the sum of several unit fractions.

For example, let’s take ¹¹⁄₁₂. The first step is to find the largest unit fraction below the other fraction. In this case, that fraction is ¹⁄₂. Then, you should subtract ¹⁄₂from ¹¹⁄₁₂, which gives ⁵⁄₁₂. This means that ¹¹⁄₁₂ = ¹⁄₂ + ⁵⁄₁₂ .  Repeat this with ⁵⁄₁₂ and you should get:

¹¹⁄₁₂ = ¹⁄₂ + ¹⁄₃ + ¹⁄₁₂

If you would like to learn more, you can to the NRICH website with these links:

https://nrich.maths.org/6540

https://nrich.maths.org/1173

https://nrich.maths.org/6541