This week, we looked at three seemingly unrelated problems which all ended up being related to binary numbers.
The first is about Russian multiplication. Take, for instance 22 x 19. Multiply the left side by 2 every time and divide the right side by 2, and do this until the right side is equal to 1. If, while you do this, you ever get a decimal number on the right side, round down to the next integer.
e.g.
| 22 |
19 |
| 44 |
9 |
| 88 |
4 |
| 176 |
2 |
| 352 |
1 |
The next step is to get rid of all the lines with an even number on the right side, which leaves us with 22, 44 and 352 on the left side. Now we know that 22 x 19 = 418. What do you notice when you add 22, 44 and 352? Now try this with other multiplications. Does it still work? If it does, can you explain why it works?
Here is a website that explain this more fully:
https://www.basic-mathematics.com/russian-peasant-multiplication.html
The second problem we looked at today was all about magic cards or maths busking. Have a look at the following cards:
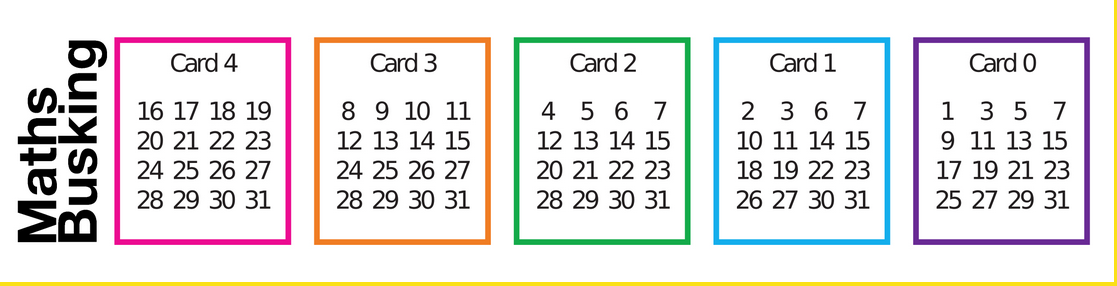
You can do the following trick with them. You ask someone to tell you which colour cards their birthdate appears on. You can straightaway say what their birthdate is. Can you guess how? It is not by learning all the numbers on the cards. One clue is to look at the first number in each card. Can you spot a pattern? Again, here is a website to help you:
http://www.mathmaniacs.org/lessons/01-binary/Magic_Trick/
Extension: If you add one more card, with how many more numbers can you do the trick with?
The final puzzle of today is about poisoned wine bottles. This is the story:
The King of a small country invites 1000 guests to his annual party.
Each guest brings the King a bottle of wine. Soon after, the Queen discovers that one of the guests is trying to assassinate the King by giving him a bottle of poisoned wine. Unfortunately, they do not know which guest, nor which bottle of wine is poisoned.
Just a single drop of the poisoned wine would kill the King.
The King has 10 prisoners in his dungeon. He decides to use them as taste testers to determine which bottle of wine contains the poison.
The poison when taken has no effect on the prisoner until exactly 24 hours later when the infected prisoner suddenly dies. The King needs to determine which bottle of wine is poisoned by tomorrow so that the festivities can continue as planned. Hence he only has time for one round of testing. How can the King administer the wine to the prisoners to ensure that 24 hours from now he is guaranteed to have found the poisoned wine bottle?
As we have seen with a lot of Maths Club problems, sometimes the first step is try with smaller numbers. For instance, instead of using 10 prisoners, we could say that there are 500 prisoners. So how could we test this now? Once you have figured this out, you could try with less and less prisoners. Now, we can solve the puzzle:
First, let’s line up our 10 prisoners and label them. Also label the wine bottles 0–999 so we can tell them apart.

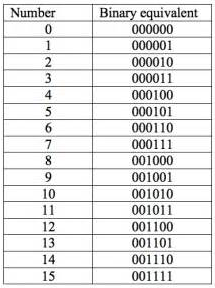
Label each bottle with both its decimal number and binary equivalent.
decimal=binary
0=0000000000
1=0000000001
2=0000000010
3=0000000011
4=0000000100
5=0000000101
6=0000000110
7=0000000111
8=0000001000
9=0000001001
10=0000001010
etc
Now each bottle serves as a code describing which prisoners are to drink from it. In this system, a one means the prisoner drinks from it, a zero means the prisoner doesn’t.
For example, only Prisoner J should drink from bottle one since its binary is 0000000001. Whereas, Prisoners I and G should drink from bottle ten whose binary is 0000001010 because it has 1’s in the columns that match up with prisoners I and G.
Continue this process until you have given out sips of wine from every bottle. After 24 hours, line up the prisoners in order and note which ones have been poisoned with ones and mark the rest with zeros. Convert this number back into decimal to reveal which bottle was poisoned.
Extension: If there were 2000 bottles, how many prisoners would you need?
If you would like to learn to learn more about binary, check out this website:
https://www.mathsisfun.com/binary-number-system.html