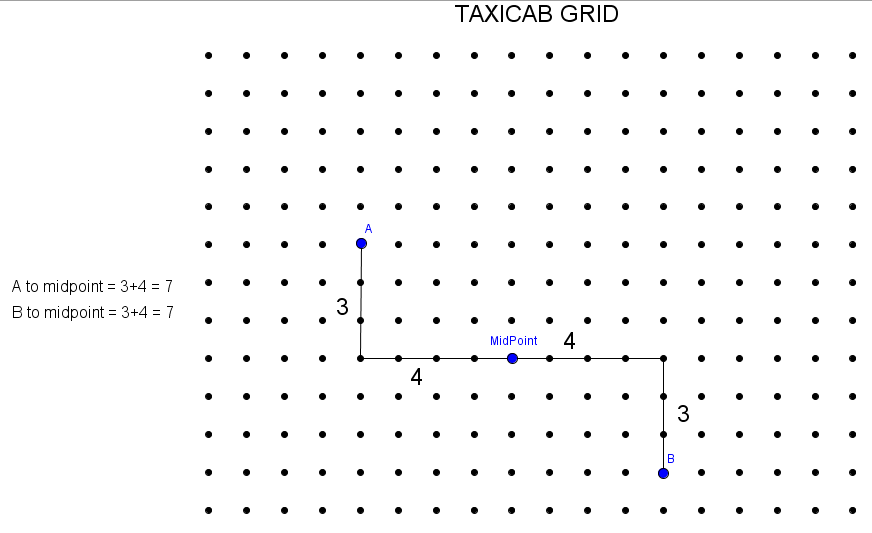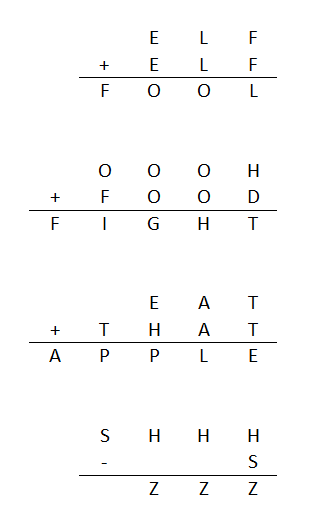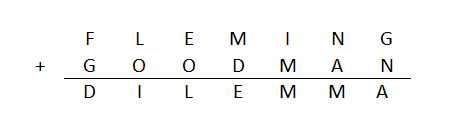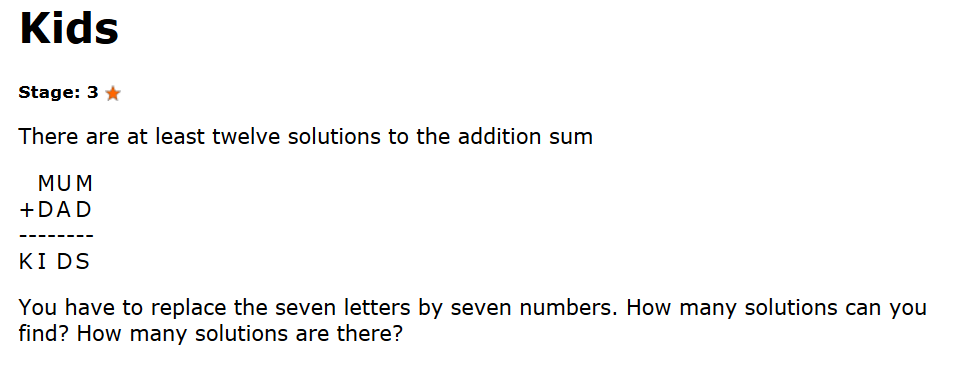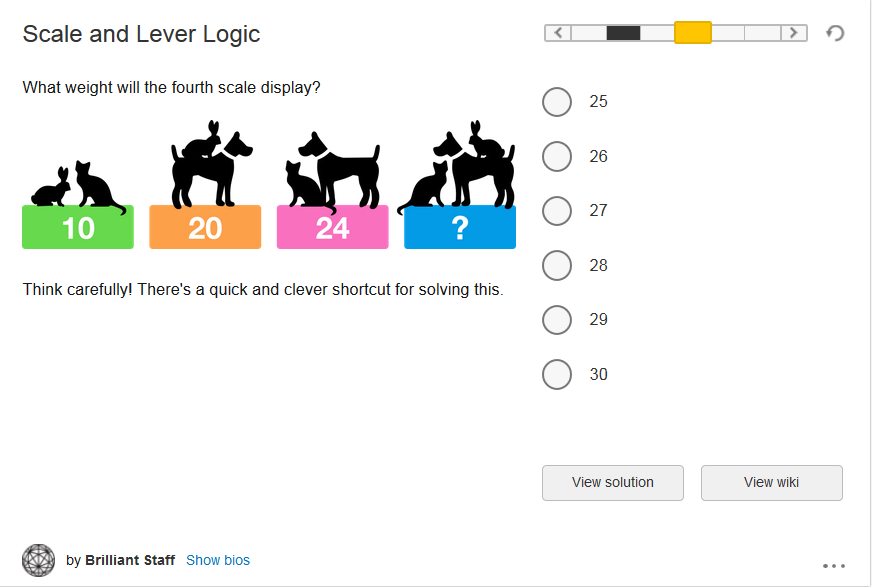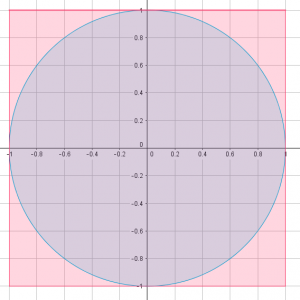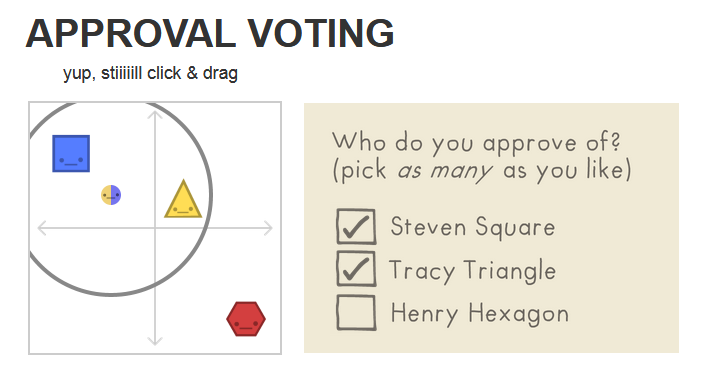
Finding betting ways to vote
We looked at different ways to decide which candidate or choice won a vote. We realised that by using different methods, different candidates won the vote. This raises the troubling question about whether our way of voting is the best and the fairest. Here is a link to the activity we did and here is a link to an interactive website that discuss precisely this question. In the UK, the voting system is relative majority. However, it could be a good thing if we use absolute majority voting, because it would allow members of smaller parties to also get a voice. This could lead to a bigger number of parties rather than two or three major parties. However, there is no perfect voting system.