

Welcome to students in from around the world. We hope you will enjoy working on these maths club activities together collaboratively via our website.
For each activity there may be specific instructions, and in general please post your solutions/hints and questions on this website.
We look forward to helping you work together across two continents!






3 sisters can never choose what to have for dinner. So they take a vote. 1 is their first choice, 5 is their least favourite. What should they have for dinner?
3 filles n’arrivent jamais à choisir quoi manger pour le dîner. Elles décident donc de faire un vote. 1 est leur premier choix, 5 leur dernier. Que devraient-elles manger pour le dîner ?
Rosie
| Food/Nourriture | Preference/Préference |
| Plaintain | 1 |
| Rice | 2 |
| Chips | 4 |
| Spaghetti | 5 |
| Ugali | 3 |
Precious
| Food/Nourriture | Preference/Préference |
| Plaintain | 5 |
| Rice | 2 |
| Chips | 3 |
| Spaghetti | 4 |
| Ugali | 1 |
Florence
| Food/Nourriture | Preference/Préference |
| Plaintain | 2 |
| Rice | 3 |
| Chips | 1 |
| Spaghetti | 4 |
| Ugali | 5 |
Which dish should their mother cook?
Quel plat devrait cuisiner leur mère ?
Can you make an argument for each of the dishes?
Peux-tu donner des arguments pour défendre chaque plat ?
Give us your suggestions in the comments section!
Donnes-nous tes suggestions dans les commentaires !
Hello everyone … we hope you will enjoy working on the problem below from the UK and Kenya! Please post your comments below.
First think of an integer written out in letters e.g. sixteen.
Take the number of letters in this number e.g. 7
Write this number out e.g. seven
Take the number of letters in this number e.g. 5
Write this number out e.g. five
Take the number of letters in this number e.g. 4
Write this number out e.g. four
Now we have converged to the number four.
Try this process with other numbers and see what happens.
Is it the same in other languages?
You may want to use the power of Python programming language to explore this further. You can make the Trinket below fullscreen by clicking on the three parallel lines in the top left corner and then clicking fullscreen (and do this again to stop it being fullscreen).

You are given two eggs, and access to a 100-storey building. Both eggs are identical. The aim is to find out the highest floor from which an egg will not break when dropped out of a window from that floor. If an egg is dropped and does not break, it is undamaged and can be dropped again. However, once an egg is broken, that’s it for that egg.
If an egg breaks when dropped from floor n, then it would also have broken from any floor above that. If an egg survives a fall, then it will survive any fall shorter than that.
The question is: What strategy should you adopt to minimize the number egg drops it takes to find the solution? (And what is the worst case for the number of drops it will take?)
Thank you everyone for your excellent contributions. Well done trying by hand and I hope some of you had a look at trying different numbers on the geogebra applet here.
It seems like finding a long sequence really is a challenge no matter what numbers you use.
However ….
It is technically possible to choose four numbers that make an infinite sequence where you never end up at 0,0,0,0. The solution is very tricky to work with though and using a computer doesn’t even help because computers round numbers to a certain number of decimal places which messes up the result.
For an explanation and how to get to the solution have a look at this blog.
The next official challenge will be launched on Wednesday 19th of April … please enjoy the other puzzles on this site in the meantime.
Deadline – 22nd of March!
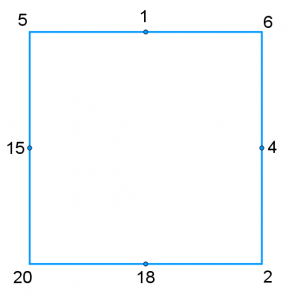
Draw a square and choose four numbers to put at each vertex. For example:

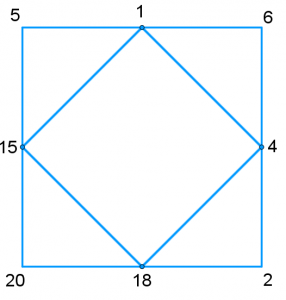
Now in the middle of each segment write the positive difference between the two numbers at each end. e.g. the difference between 5 and 6 is 1.
Join these new points up with a square
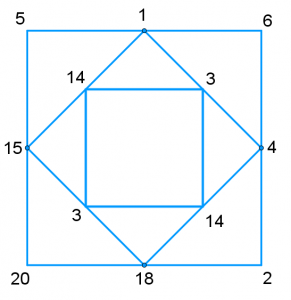
Now in the middle of each segment of the new square find the positive difference of the numbers at each end. For example the difference between 15 and 1 is 14. Do this for all the segments and draw another square joining up your four new answers.
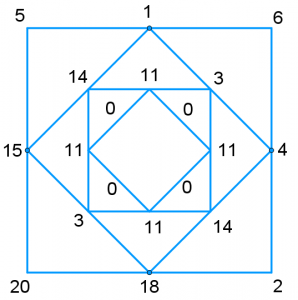
Keep finding the positive differences and joining these points up into a square until you reach 0,0,0,0.
Choose four new starting numbers and follow the instructions above to create your own version of this.
Our first choice of four starting numbers meant drawing 4 squares before we reached 0,0,0,0. How many squares have you drawn with your choice of starting numbers?
Your challenge is now to find the longest sequence of squares you can before the sequence reaches 0,0,0,0 and send us your answer.
An easy way to send sequences would be as lists of numbers. For example the one above could be written as

Please write giving us your longest sequence and any other thoughts on the puzzle using the “Leave a comment” button below.