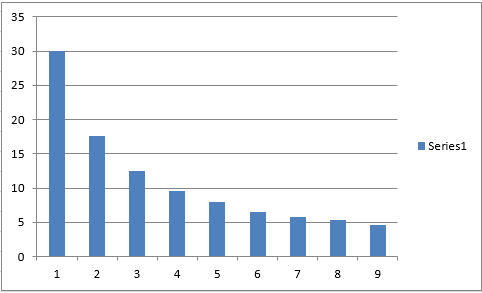
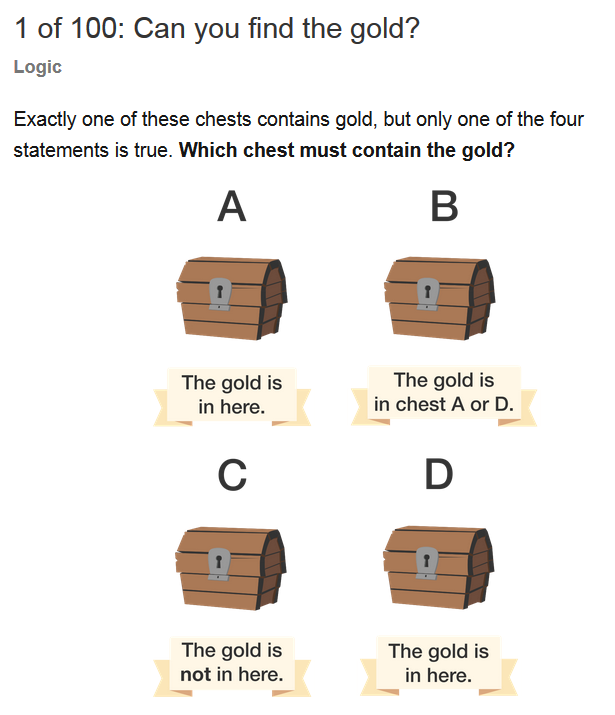
You are on one side of a river, and with you, there is a wolf, a goat and a cabbage. You have one boat, and can only take one living thing at a time. The goat cannot be left alone with the cabbage and the wolf cannot be left alone with the goat. How many journeys must you do in minimum to get all the objects to the other side of the river? In how many different ways can you do it?
Here is a very interesting way to look at the problem which involves representing the problem in 3D wolf/goat/cabbage space.
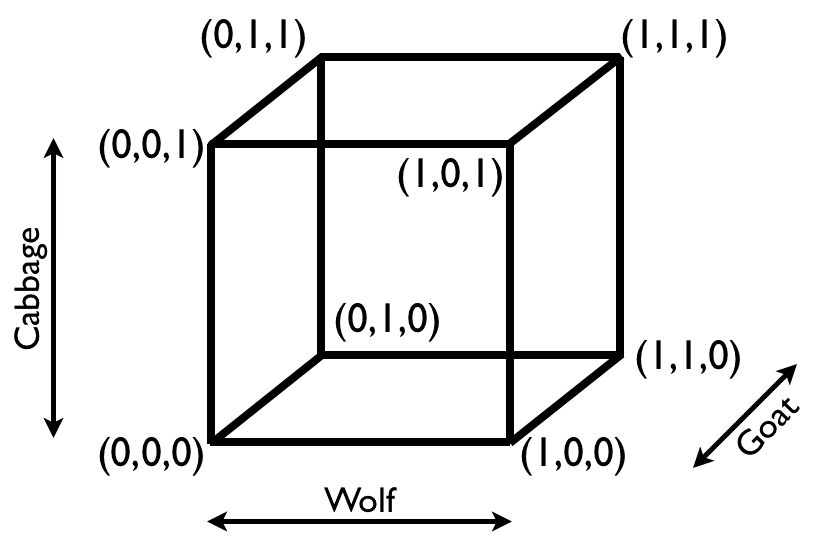
The problem is then changed to getting from one vertex of the cube to another.
Finally, we looked at another river crossing puzzle, this time involving wildebeest and lions. This puzzle is fully explained and answered in this Ted-Ed talk.
Before looking at how they propose to solve the puzzle, how did you go about solving it?