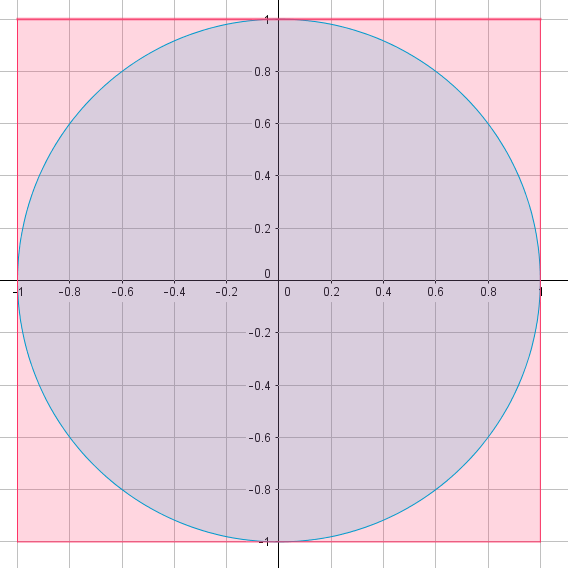
This week we ran a treasure hunt round the school and a pi recital competition and in maths club we used Geogebra to estimate pi .

This week we ran a treasure hunt round the school and a pi recital competition and in maths club we used Geogebra to estimate pi .
We did some computer programming with Python today in maths club – using the brilliant Code Club website.
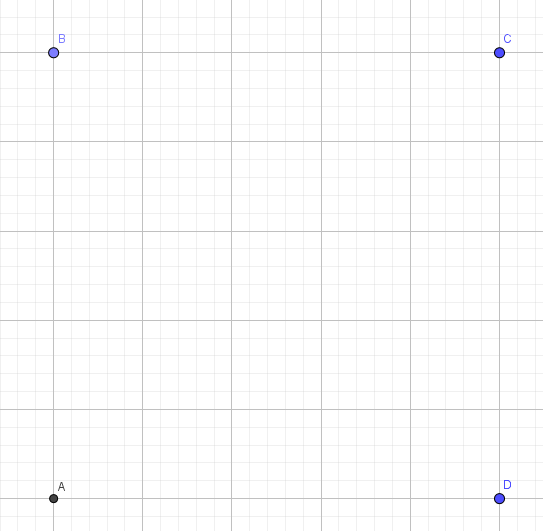
Imagine four towns in a square system with side length 1 mile.
You would like to connect all four towns by motorways, using the least amount of road (not necessarily the most efficient for any one particular town).
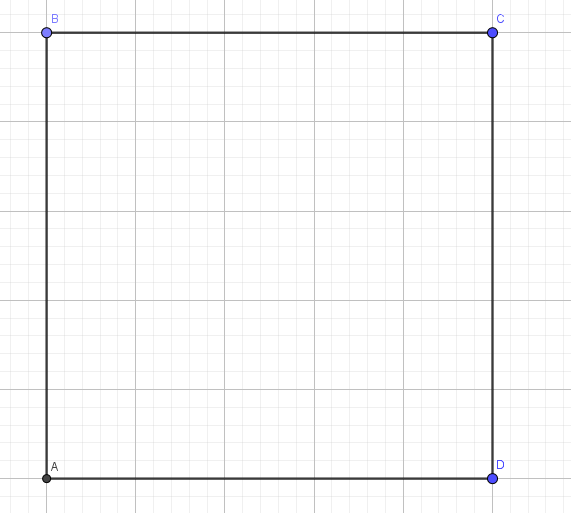
Here is one option – it would take 4 miles of road. Can you do better?
Once you have had plenty of time to think and try and find and evaluate the best route, watch this video for the solution.

Today we played a great Nigerian game called Dara.
A printable board and the rules can be found here.

The rules of a secret santa are that each person’s name is put in a hat and the names are mixed. Then each person must choose 1 name from the hat. If you choose your own name, you must put it back in the hat.
If 2 people do a secret santa there is only one solution: Person A gives to person B and person B gives to person A.
Stage 1: With 3 people, there are 2 possible ways. Can you think why?
Stage 2: Now how many different ways are there with 4 people?
The final challenge is to find the number of different scenarios with 5 people.
Solutions can be found here.

Did you know genuine snowflakes have six fold symmetry? We learnt this and more using the resources by Matt Parker here.

Today we worked on all our Christmas cracker puzzles.

Today we looked at ways to count on our fingers. Up to 10 is obviously straight forward, but can you do better?
We managed 1023. Can you work out how? Can you do better?
This idea came from a great maths book – Things to Make and Do in the Fourth Dimension This website link has lots of gadgets to play with.