Pick’s Theorem

We worked on ideas from this NRich activity today.

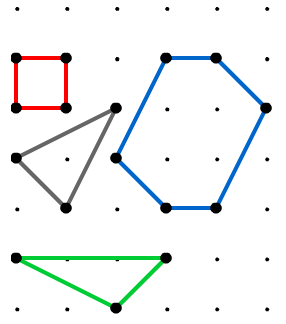
When the dots on square dotty paper are joined by straight lines the enclosed figures have dots on their perimeter (a) and often internal (b) ones as well.

Figures can be described in this way: (a,b).
For example, the red square has an (a,b) of (4,0), the grey triangle (3,1), the green triangle (5,0) and the blue hexagon (6,4):

Questions:

1. Can you draw all (4,0) shapes?
2. Can you draw all (5,0) shapes?
3. Can you draw all (4,1) shapes?
4. Can you draw all (4,2) shapes?
5. Can you draw various shapes with area 4cm²
6. What do you notice about the area of the shapes from your work on questions 1-4?
7. Can you come up with a formula for the Area in terms of a and b?

Here are our solutions.

For more info on this theorem see the solutions in the Nrich activity and watch this brilliant proof.