We were inspired by this Numberphile video by Neil Sloane today.
Starting with 2 ones, what is the maximum number you can place on an infinite grid according to the rule:
“You can place a number if all the numbers immediately around it add up to itself”
Here is a way to get up to 4:
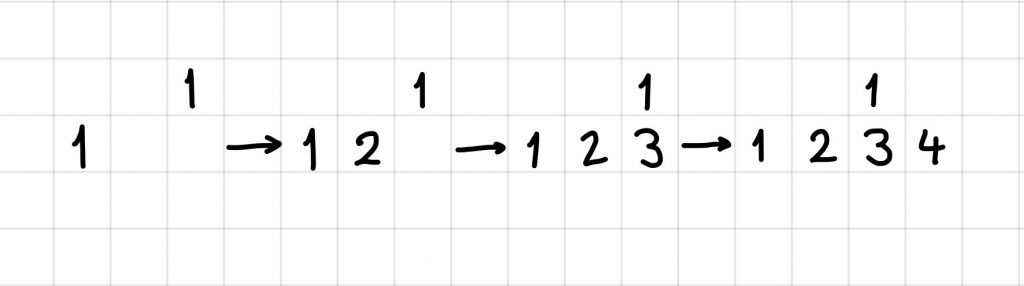
But then we are stuck as there is nowhere to put the 5. Can you do better than 4?
You can choose where to place the 2 ones to start with, for example:

or

This puzzle can be tried with any number of 1s to start with.
What is the maximum number you can place starting with three 1s?
If the maximum number you can reach is a(n) for n starting 1s, an interesting question is what is the best lower bound we can find for a(n).
Imagine this diagram continuing …
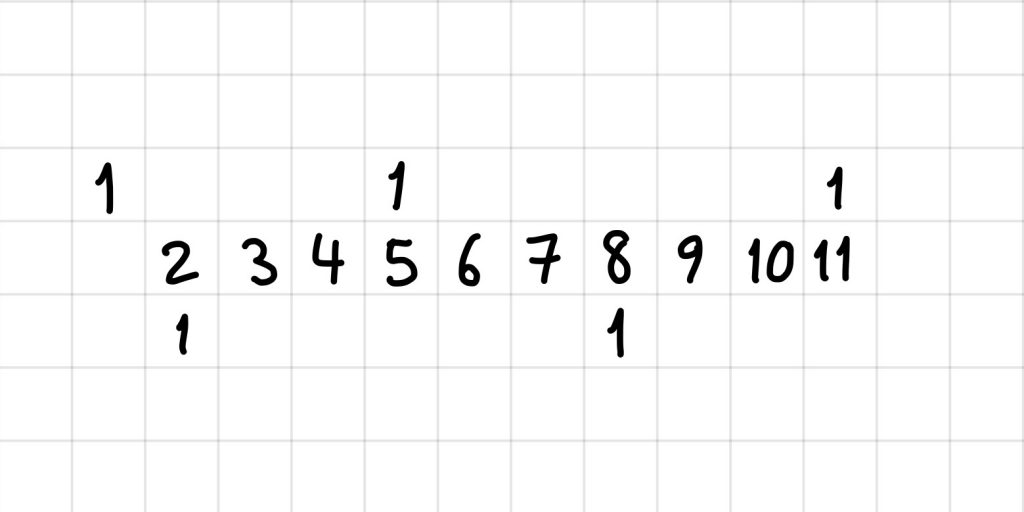
If we split it into sections we have demonstrated that a(n)>=3n-3
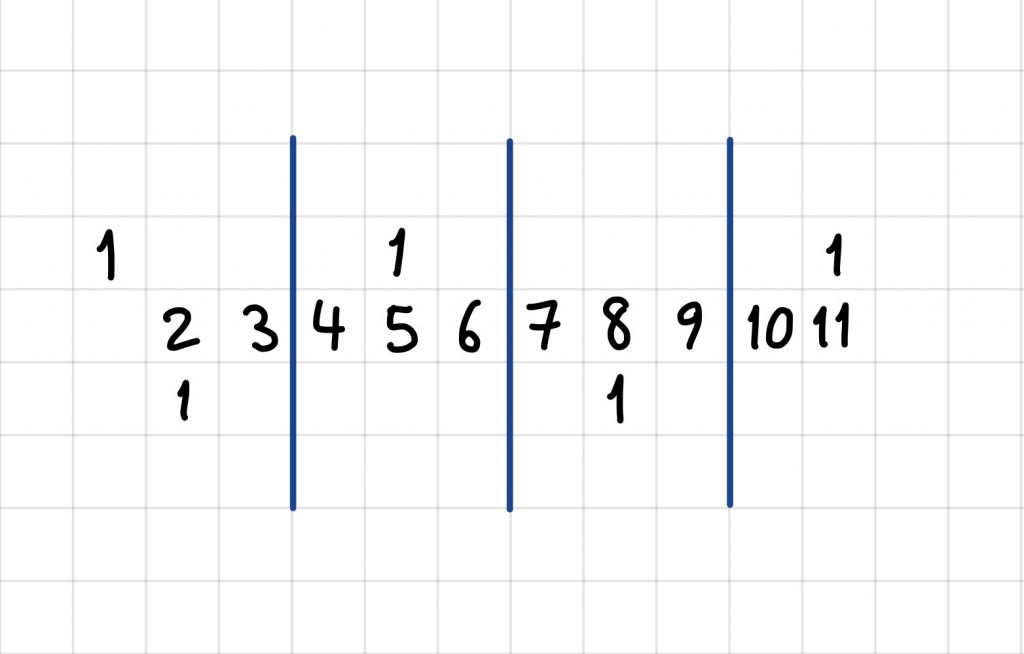
Can you find a higher lower bound for a(n) by drawing a different pattern that would continue indefinitely?