You might be familiar with divisibility rules such as “A number is divisible by 3 if the sum of the digits is divisible by 3”. You can see some more here.
Our investigation today was – can we develop a set of divisibility rules for binary numbers?
Divisible by 2
This was straightforward. If the rightmost (unit) digit is 0 then the number is divisible by 2.
e.g. The number 6 is divisible by 2
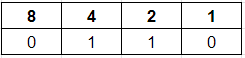
but the number 7 is not
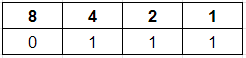
Can you extend this logic to create a divisibility rule for powers of 2 (e.g. 4, 8, 16 …)? Solution