Practical Numbers

This activity was inspired by this numberphile video.
20 is a practical number because it could be used to design a set of weights where all of its factors are the weights and you can weigh all the numbers from 1 to 20 using each weight only once.
The factors of 20 are: 1, 2, 4, 5, 10 and 20
And you can make the numbers 1 to 20 using combinations of these numbers (each number can be used a maximum of once):
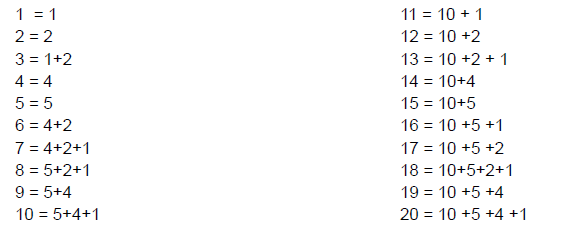
So 20 is a practical number
Of course all powers of 2 are practical numbers, but can you find some others?
Do they have anything in common?
Are there an infinite number of practical numbers?
Once you’ve found some can you use them to generate more?
Using these facts:
- The product of two practical numbers is also a practical number.
- More strongly, the least common multiple of any two practical numbers is also a practical number.
- if n is a practical number and d is one of its divisors then d must also be a practical number.
So for example with the primitive practical numbers 1 and 2 you can generate 2*2=4
So 4 is not a primitive number as it can be generated from previous ones.
Can you circle all the practical numbers in this grid, using a different colour for primitive practical numbers?
Solution can be found here. To read more about Practical Numbers check out Wikipedia and this talk.
Using Python
Task 1
https://trinket.io/python/c9f4762222
Change the program so that the factors are given in a list (you can use e.g. factors.append(i) after setting up a blank list called factors
Task 2 – change the program so that instead of asking the user for a number it displays the factors of all the numbers from 1 to 30.
Task 3
totals=[]
factors=[“a”,”b”,”c”,”d”]
Write a program that starts as above and prints this:
[‘a’, ‘b’, ‘c’, ‘d’, ‘ab’, ‘ac’, ‘ad’, ‘bc’, ‘bd’, ‘cd’, ‘abc’, ‘abd’, ‘acd’, ‘bcd’, ‘abcd’]
This is a starting point if you are stuck.
Task 4
Adapt your program for Task 3 to work with any factor list up to 7
Solution to Task 4 up to length 7
Chatgpt solution for any length!
Task 5
Combine your programs from Task 2 and Task 4 to list all the totals that can be made with the factors of numbers from 1 and 30.
It should display like this:
The factors of 1 are:
[1]
and all the totals you can make are:
[1]
The factors of 2 are:
[1, 2]
and all the totals you can make are:
[1, 2, 3]
The factors of 3 are:
[1, 3]
and all the totals you can make are:
[1, 3, 4]
The factors of 4 are:
[1, 2, 4]
and all the totals you can make are:
[1, 2, 4, 3, 5, 6, 7]
You can use this code to print a new line:
print(“\n”)
Task 6
Find all the practical numbers between 1 and 30
Task 7
Watch this numberphile video!
Task 8
After watching the video can you think of some improvements to make your code more efficient?