Month: March 2024

We tried this fun game today in maths club and then started to code it. See this previous post for similar code to adapt.

Breaking news!!!! You can now do python on Geogebra. Try it out here. And here is an article about it.

Could you adapt the program above to make a nice tesselation of hexagons?

Or you could try squares to start with? Here is a solution for squares.

Also check out the examples on the site by going to File – Open – Examples

We did this brilliant activity from Think Maths and Matt Parker using dice and excel

Practical Numbers

This activity was inspired by  this numberphile video.

20 is a practical number because it could be used to design a set of weights where all of its factors are the weights and you can weigh all the numbers from 1 to 20 using each weight only once.

The factors of 20 are: 1, 2, 4, 5, 10 and 20

And you can make the numbers 1 to 20 using combinations of these numbers (each number can be used a maximum of once):

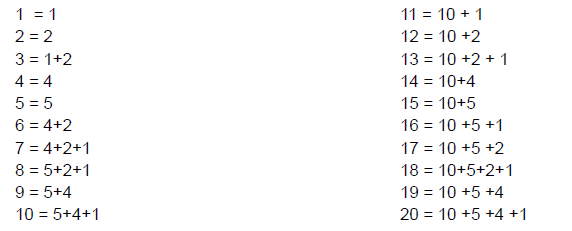
So 20 is a practical number

Of course all powers of 2 are practical numbers, but can you find some others?

Do they have anything in common?

Are there an infinite number of practical numbers?

Once you’ve found some can you use them to generate more?

Using these facts:

• The product of two practical numbers is also a practical number.
• More strongly, the least common multiple of any two practical numbers is also a practical number.
• if n is a practical number and d is one of its divisors then d must also be a practical number.

So for example with the primitive practical numbers 1 and 2 you can generate 2*2=4 

So 4 is not a primitive number as it can be generated from previous ones.

Can you circle all the practical numbers in this grid, using a different colour for primitive practical numbers?

Solution can be found here. To read more about Practical Numbers check out Wikipedia and this talk.

Using Python

Task 1

https://trinket.io/python/c9f4762222

 Change the program so that the factors are given in a list (you can use e.g. factors.append(i) after setting up a blank list called factors 

Solution to Task 1

Task 2 – change the program so that instead of asking the user for a number it displays the factors of all the numbers from 1 to 30.

Solution to Task 2 

Task 3 

totals=[]

factors=[“a”,”b”,”c”,”d”]

Write a program that starts as above and prints this:

[‘a’, ‘b’, ‘c’, ‘d’, ‘ab’, ‘ac’, ‘ad’, ‘bc’, ‘bd’, ‘cd’, ‘abc’, ‘abd’, ‘acd’, ‘bcd’, ‘abcd’]

This is a starting point if you are stuck.

Solution to Task 3

Task 4 

Adapt your program for Task 3 to work with any factor list up to 7

Solution to Task 4 up to length 7

Chatgpt solution for any length! 

Task 5

Combine your programs from Task 2 and Task 4 to list all the totals that can be made with the factors of numbers from  1 and 30.

It should display like this:

The factors of 1 are:

[1]

and all the totals you can make are:

[1]

The factors of 2 are:

[1, 2]

and all the totals you can make are:

[1, 2, 3]

The factors of 3 are:

[1, 3]

and all the totals you can make are:

[1, 3, 4]

The factors of 4 are:

[1, 2, 4]

and all the totals you can make are:

[1, 2, 4, 3, 5, 6, 7]

You can use this code to print a new line:

print(“\n”)

Solution to Task 5

Task 6

Find all the practical numbers between 1 and 30

Solution to Task 6 

Alternative solution that you can use to find all the practical numbers up to your choice of max number

Task 7

Watch this numberphile video!

Task 8

After watching the video can you think of some improvements to make your code more efficient?