Month: January 2024

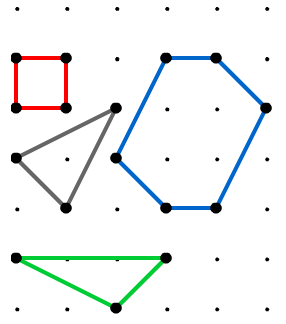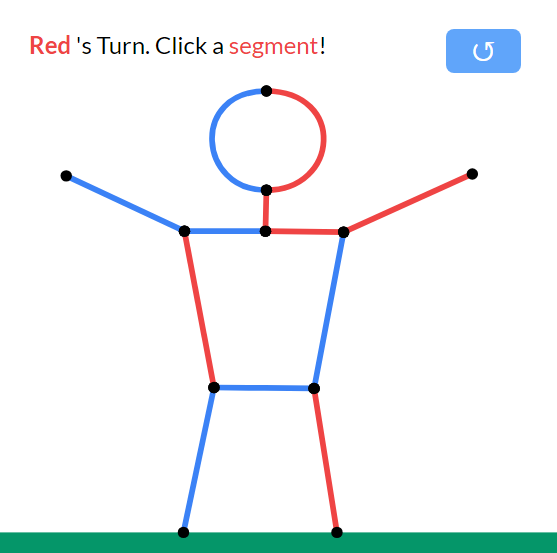
This fun two player game has a lot of strategies to consider …

The rules (from Wikipedia) are

Each line segment is coloured either red or blue. One player (usually the first, or left, player) is only allowed to cut blue line segments, while the other player (usually the second, or right, player) is only allowed to cut red line segments.

On their turn, a player “cuts” (erases) any line segment of their choice. Every line segment no longer connected to the ground by any path “falls” (i.e., gets erased). According to the normal play convention of combinatorial game theory, the first player who is unable to move loses.

Try it out here.

Can you create your own starting grids so that …

Player blue wins, regardless of if they go first or second 

Player 1 wins, regardless of if they are red or blue 

Player 2 wins, regardless of if they are red or blue  

They might not all be possible!

Lots more to read here.

It is also interesting to analyse the “game value”, for example:

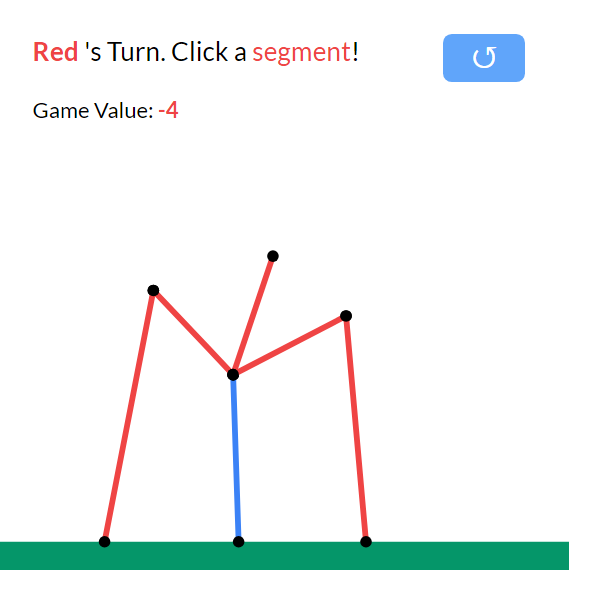
For some ideas on how to calculate the game value see this exploration.

We worked on ideas from this NRich activity today.

When the dots on square dotty paper are joined by straight lines the enclosed figures have dots on their perimeter (a) and often internal (b) ones as well.

Figures can be described in this way: (a,b).
For example, the red square has an (a,b) of (4,0), the grey triangle (3,1), the green triangle (5,0) and the blue hexagon (6,4):

Questions:

1. Can you draw all (4,0) shapes?
2. Can you draw all (5,0) shapes?
3. Can you draw all (4,1) shapes?
4. Can you draw all (4,2) shapes?
5. Can you draw various shapes with area 4cm²
6. What do you notice about the area of the shapes from your work on questions 1-4?
7. Can you come up with a formula for the Area in terms of a and b?

Here are our solutions.

For more info on this theorem see the solutions in the Nrich activity and watch this brilliant proof.

We played the great game of SET and then answered these questions. The answers can be found in this document from The Madison Math Circle. Thanks to them and David J Bruce for the ideas.

We also started to think about how to represent cards in a geometric space. If you take a simple game of set with just two characteristics, you can plot each card in 2D and hence work out how many cards you can have on the table before you make a set (by not drawing a straight line). See here for the details.

The Irish logarithm is an algorithm invented by Percy Ludgate in 1909 for multiplying single-digit numbers. The idea was to program a computer to do these calculations.
The algorithm uses two tables to perform the multiplication. With just these tables you can calculate products up to 9×9 simply by adding two numbers together.

Here are blank versions of the two tables below (and as a pdf).

Our challenge was to fill in these tables. Here is the start of an attempt that would not work …

1 x 2 would be 1+2 so the correct answer of 2 needs to be in the box called 3.

1×3 would be 1+3 so the correct answer of 3 needs to be in the box called 4.

2×3 would be 2+3 so the correct answer of 6 needs to be in the box called 5.

So far so good ….

But … 2×2 would be 2+2 so the correct answer of 4 needs to go in the box called 4. But the box called 4 already has a 3 in it, so our initial choice of numbers is a bad one.

Can you do better?

It is very difficult to come up with the solution from scratch (but do try!). Here are a few numbers already filled in, if you would like a starting point (and as a pdf).

The solution is not unique, but here is Ludgate’s solution (and as a pdf).