Taxicab geometry is a form of geometry, where the distance between two points A and B is not the length of the line segment AB but the sum of the shortest horizontal and vertical distances between the two points. Imagine you are in a taxi in New York – you can’t go through buildings! Example:
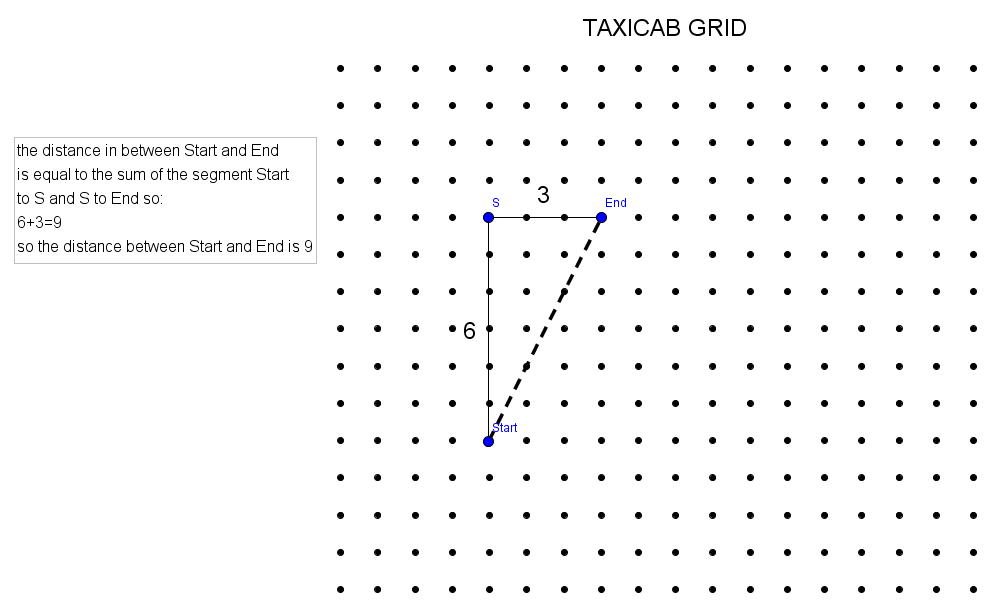
The first challenge is to try to find what a midpoint would be in taxicab geometry. Here is an example to help:
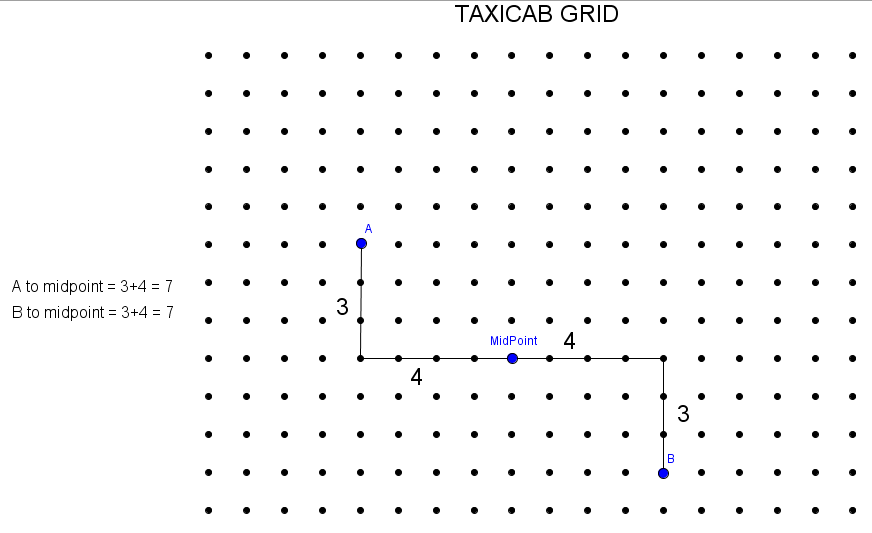
Since the distance between A to the midpoint is the same as the distance between the point B and the midpoint, the midpoint is at the same distance from A and B. Can you spot any more midpoints, if there are any? Can you pick two different points that do not have a midpoint?
The second task is to find what a perpendicular bisector looks like on taxicab geometry.
The third task is to try to draw a circle in the taxicab geometry.
Next, try to draw an equilateral triangle and a rhombus.
For more info have a look here.