Month: October 2017

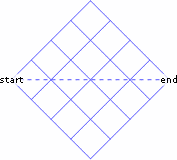
This week’s problem is all about counting the number of paths from one point to another on a 4 by 4 grid.

You can only travel in these directions

Here is one acceptable path:

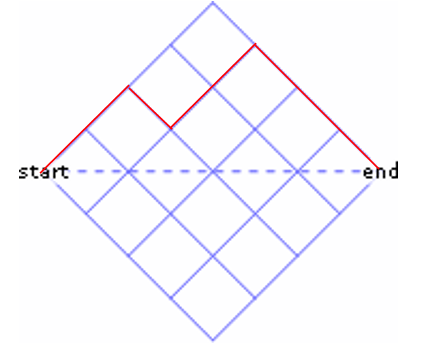
So how many such paths are there? First off, in which of these ranges do you think the answer lies:

< 20
20 – 40
40 – 60
60 – 80
80 – 100
>100

A first tip on how to solve this is to look at what is going on with smaller grids. Why don’t we start with a 1 by 1 grid? How many different paths are there between the starting point and the end point? Once we have done that, we can place the data on our larger grid.

After doing this a few times, does a pattern start to emerge?

Here is a website that shows all the solutions and an explanation of how the problem works, if you would like to learn more.

http://www.robertdickau.com/lattices.html

Today, we looked at an interesting problem taken from the NRICH website, involving visualisation and cubes covered in ink. If you go to this link, you can find all the details of the problem and some solutions:

https://nrich.maths.org/7241

However, this is quite an open problem and so there may be more than one solution…

You are on one side of a river, and with you, there is a wolf, a goat and a cabbage. You have one boat, and can only take one living thing at a time. The goat cannot be left alone with the cabbage and the wolf cannot be left alone with the goat. How many journeys must you do in minimum to get all the objects to the other side of the river? In how many different ways can you do it?

Here is a very interesting way to look at the problem which involves representing the problem in 3D wolf/goat/cabbage space.

The problem is then changed to getting from one vertex of the cube to another.

Finally, we looked at another river crossing puzzle, this time involving wildebeest and lions. This puzzle is fully explained and answered in this Ted-Ed talk.

Before looking at how they propose to solve the puzzle, how did you go about solving it?

The first task of today was if numbers were chosen at random, what would be the probability that numbers started with the digits 1 to 9. Of course the probability would be the same for each digit.

Ok, let’s see if this works. Go ahead and find any article, it can be a news article, a scientific article, etc. Now count the number of times that each digit 1 to 9 is at the start of a number. Does the distribution seem even?

Let’s see if this trend can be found in mathematical sequences too. Here’s an example: the Fibonacci sequence.

1,1,2,3,5,8, …

Let’s find the probability of numbers starting with digits 1 to 9 in the first 10,000 numbers of this sequence.

Quick tip: you can use excel to do this and then use the countif function to find the distribution of probabilities of numbers that start with each digit. Does the distribution seem even?

This strange pattern of occurrence is called Benford’s law, and it is very counter-intuitive.

If you would like to learn more, click on this link: https://brilliant.org/wiki/benfords-law/

So here is your final challenge: every single time you see a number today, write it down and you can then verify the law for yourself. How close did you get?