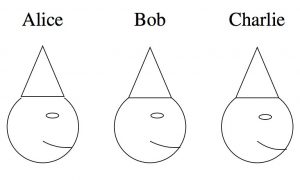
Hat puzzles provide endless entertainment! The following ones which accompany the picture above are taken directly this week’s Monday puzzle in the guardian by Alex Bellos , which is an excellent source of maths puzzles.
Alice, Bob and Charlie are well-known expert logicians; they always tell the truth. They are sat in a row, as illustrated above. In each of the scenarios below, their father puts a red or blue hat on each of their heads. Alice can see Bob’s and Charlie’s hats, but not her own; Bob can see only Charlie’s hat; Charlie can see none of the hats. All three of them are aware of this arrangement.
(i) Their father puts a hat on each of their heads and says: “Each of your hats is either red or blue. At least one of you has a red hat.” Alice then says “I know the colour of my hat.” What colour is each person’s hat?
(ii) Their father puts a new hat on each of their heads and again says: “Each of your hats is either red or blue. At least one of you has a red hat.” Alice then says “I don’t know the colour of my hat.” Bob then says “I don’t know the colour of my hat.” What colour is Charlie’s hat?
(iii) Their father puts a new hat on each of their heads and says: “Each of your hats is either red or blue. At least one of you has a red hat, and at least one of you has a blue hat.” Alice says “I know the colour of my hat.” Bob then says “Mine is red.” What colour is each person’s hat?
(iv) Their father puts a new hat on each of their heads and says: “Each of your hats is either red or blue. At least one of you has a red hat, and at least one of you has a blue hat.” Alice then says “I don’t know the colour of my hat.” Bob then says “My hat is red”. What colour is Charlie’s hat?
(v) Their father puts a new hat on each of their heads and says: “Each of your hats is either red or blue. Two of you who are seated adjacently both have red hats.” Alice then says “I don’t know the colour of my hat.” What colour is Charlie’s hat?
Answers can be found here
Another great puzzle is:
Four prisoners are arrested for a crime, but the jail is full and the jailer has nowhere to put them. He eventually comes up with the solution of giving them a puzzle so if they succeed they can go free but if they fail they are executed.
The jailer seats three of the men into a line. The fourth man is put behind a screen (or in a separate room). He gives all four men party hats. The jailer explains that there are two black hats and two white hats, that each prisoner is wearing one of the hats, and that each of the prisoners see only the hats in front of him but neither on himself nor behind him. The fourth man behind the screen can’t see or be seen by any other prisoner. No communication among the prisoners is allowed.
If any prisoner can figure out what color hat he has on his own head with 100% certainty (without guessing) and tell the jailer, all four prisoners go free. If any prisoner suggests an incorrect answer, all four prisoners are executed. The puzzle is to find how the prisoners can escape, regardless of how the jailer distributes the hats.
Answer is here.
And finally the super tricky one:
100 prisoners are lined up by an executioner, who places a red or blue hat upon each of their heads.
The prisoners can see the hats of the people lined up in from of them, but they cannot look at the hats behind them, or at their own.
Starting at the back of the line, the executioner asks the last prisoner to state the colour of his hat.
In order to live, the prisoner must answer correctly.
The night before the line-up, the prisoners can discuss a strategy to help them survive. How many prisoners can be guaranteed to be saved?
See here for a discussion of the solution.